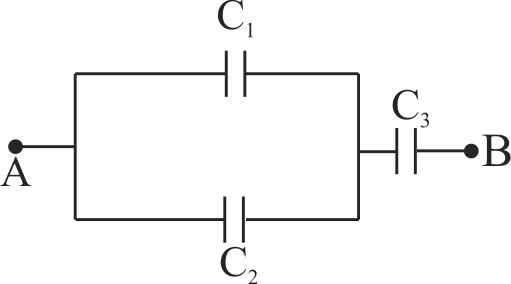
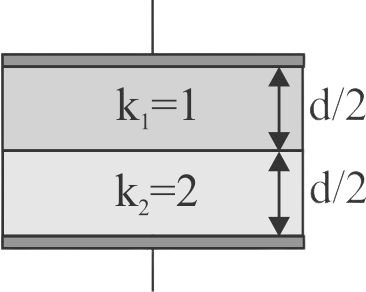
359177 Between the plates of a parallel plate condenser, a plate of thickness \({t_1}\) and dielectric constant \({K_1}\) is placed. In the rest of the space, there is another plate of thickness \({t_2}\) and dielectric constant \({K_2}.\) The potential difference across the condenser will be
359178
A parallel plate capacitor is made of two dielectric blocks. One of the blocks has thickness \({d_1}\) and dielectric constant \({K_1}\) and the other has thickness \({d_2}\) and dielectric constant \({K_2}\) as shown in figure. This arrangement can be thought as a dielectric slab of thickness \(\left( {d = {d_1} + {d_2}} \right)\) and effective dielectric constant \(K\). The \(K\) is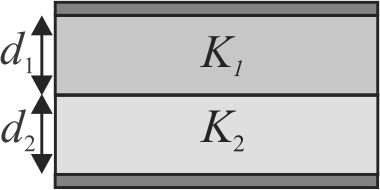
359177 Between the plates of a parallel plate condenser, a plate of thickness \({t_1}\) and dielectric constant \({K_1}\) is placed. In the rest of the space, there is another plate of thickness \({t_2}\) and dielectric constant \({K_2}.\) The potential difference across the condenser will be
359178
A parallel plate capacitor is made of two dielectric blocks. One of the blocks has thickness \({d_1}\) and dielectric constant \({K_1}\) and the other has thickness \({d_2}\) and dielectric constant \({K_2}\) as shown in figure. This arrangement can be thought as a dielectric slab of thickness \(\left( {d = {d_1} + {d_2}} \right)\) and effective dielectric constant \(K\). The \(K\) is
359177 Between the plates of a parallel plate condenser, a plate of thickness \({t_1}\) and dielectric constant \({K_1}\) is placed. In the rest of the space, there is another plate of thickness \({t_2}\) and dielectric constant \({K_2}.\) The potential difference across the condenser will be
359178
A parallel plate capacitor is made of two dielectric blocks. One of the blocks has thickness \({d_1}\) and dielectric constant \({K_1}\) and the other has thickness \({d_2}\) and dielectric constant \({K_2}\) as shown in figure. This arrangement can be thought as a dielectric slab of thickness \(\left( {d = {d_1} + {d_2}} \right)\) and effective dielectric constant \(K\). The \(K\) is
359177 Between the plates of a parallel plate condenser, a plate of thickness \({t_1}\) and dielectric constant \({K_1}\) is placed. In the rest of the space, there is another plate of thickness \({t_2}\) and dielectric constant \({K_2}.\) The potential difference across the condenser will be
359178
A parallel plate capacitor is made of two dielectric blocks. One of the blocks has thickness \({d_1}\) and dielectric constant \({K_1}\) and the other has thickness \({d_2}\) and dielectric constant \({K_2}\) as shown in figure. This arrangement can be thought as a dielectric slab of thickness \(\left( {d = {d_1} + {d_2}} \right)\) and effective dielectric constant \(K\). The \(K\) is
359177 Between the plates of a parallel plate condenser, a plate of thickness \({t_1}\) and dielectric constant \({K_1}\) is placed. In the rest of the space, there is another plate of thickness \({t_2}\) and dielectric constant \({K_2}.\) The potential difference across the condenser will be
359178
A parallel plate capacitor is made of two dielectric blocks. One of the blocks has thickness \({d_1}\) and dielectric constant \({K_1}\) and the other has thickness \({d_2}\) and dielectric constant \({K_2}\) as shown in figure. This arrangement can be thought as a dielectric slab of thickness \(\left( {d = {d_1} + {d_2}} \right)\) and effective dielectric constant \(K\). The \(K\) is