359235
A parallel plate capacitor is made of two plates of length \(l\), width \(W\) and separated by distance \(d\). A dielectric slab (dielectric constant \(K\)) that fits exactly between the plates is held near the edge of the plates. It is pulled into the capacitor by a force \({\mathop{\rm F}\nolimits} = - \frac{{\partial U}}{{\partial {\rm{x}}}}\) where \(U\) is the energy of the capacitor when dielectric is inside the capacitor up to distance \(x\) (See figure). If the charge on the capacitor is \(Q\) then the force on the dielectric when it is near the edge is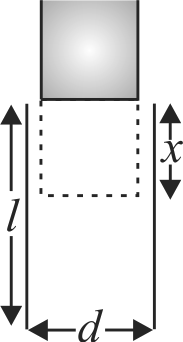
359236 Two condensers of capacities 2\(C\) and \(C\) are joined in parallel and charged upto potential \(V\). The battery is removed and the condenser of capacity \(C\) is filled completely with a medium of dielectric constant \(K\). The \(p\).\(d\). across the capacitors will now be
359235
A parallel plate capacitor is made of two plates of length \(l\), width \(W\) and separated by distance \(d\). A dielectric slab (dielectric constant \(K\)) that fits exactly between the plates is held near the edge of the plates. It is pulled into the capacitor by a force \({\mathop{\rm F}\nolimits} = - \frac{{\partial U}}{{\partial {\rm{x}}}}\) where \(U\) is the energy of the capacitor when dielectric is inside the capacitor up to distance \(x\) (See figure). If the charge on the capacitor is \(Q\) then the force on the dielectric when it is near the edge is
359236 Two condensers of capacities 2\(C\) and \(C\) are joined in parallel and charged upto potential \(V\). The battery is removed and the condenser of capacity \(C\) is filled completely with a medium of dielectric constant \(K\). The \(p\).\(d\). across the capacitors will now be
359235
A parallel plate capacitor is made of two plates of length \(l\), width \(W\) and separated by distance \(d\). A dielectric slab (dielectric constant \(K\)) that fits exactly between the plates is held near the edge of the plates. It is pulled into the capacitor by a force \({\mathop{\rm F}\nolimits} = - \frac{{\partial U}}{{\partial {\rm{x}}}}\) where \(U\) is the energy of the capacitor when dielectric is inside the capacitor up to distance \(x\) (See figure). If the charge on the capacitor is \(Q\) then the force on the dielectric when it is near the edge is
359236 Two condensers of capacities 2\(C\) and \(C\) are joined in parallel and charged upto potential \(V\). The battery is removed and the condenser of capacity \(C\) is filled completely with a medium of dielectric constant \(K\). The \(p\).\(d\). across the capacitors will now be
359235
A parallel plate capacitor is made of two plates of length \(l\), width \(W\) and separated by distance \(d\). A dielectric slab (dielectric constant \(K\)) that fits exactly between the plates is held near the edge of the plates. It is pulled into the capacitor by a force \({\mathop{\rm F}\nolimits} = - \frac{{\partial U}}{{\partial {\rm{x}}}}\) where \(U\) is the energy of the capacitor when dielectric is inside the capacitor up to distance \(x\) (See figure). If the charge on the capacitor is \(Q\) then the force on the dielectric when it is near the edge is
359236 Two condensers of capacities 2\(C\) and \(C\) are joined in parallel and charged upto potential \(V\). The battery is removed and the condenser of capacity \(C\) is filled completely with a medium of dielectric constant \(K\). The \(p\).\(d\). across the capacitors will now be