Explanation:
There are two independent loops in the circuit as shown in the figure.
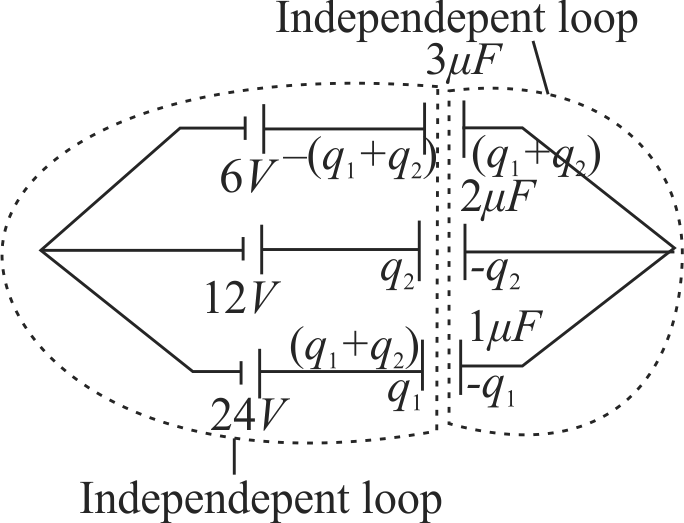
To find two unknown variables we write Kirchoff’s laws in any two closed loops.
\(24V - \frac{{{q_1}}}{{1\mu F}} + \frac{{{q_2}}}{{2\mu F}} - 12V = 0\)
\(12V - \frac{{{q_1}}}{{1\mu F}} + \frac{{{q_2}}}{{2\mu F}} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\)
\(24V - \frac{{{q_2}}}{{1\mu F}} - \frac{{({q_1} + {q_2})}}{{3\mu F}} - 6V = 0\)
\(18V - \frac{{{q_2}}}{{1\mu F}} - \frac{{({q_1} + {q_2})}}{{3\mu F}} = 0\,\,\,\,\,\,\,(2)\)
From Eq’s (1) & (2) we get
\({q_1} = 16\mu C\,\,\& \,\,{q_2} = 8\mu C\)
\({V_a} - {V_b} = - \frac{{({q_1} + {q_2})}}{{3\mu F}} - 6V = - 14V\)