366264 Moment of inertia of a body about given axis is \(2.4\;kg\;{m^2}\). Initially it is at rest. An angular acceleration of \(25\,rad/{s^2}\) is applied on it for \(t_{0}\) time so that its rotational kinetic energy becomes 1500 joule. The \(t_{o}\) is

366265 A body of mass \(1\,kg\) is suspended by a weightless string which passes over a frictionless pulley of mass \(2\,kg\) as shown in the figure. The mass is released from a height of \({1.6 m}\) from the ground. With what velocity does it strike the ground?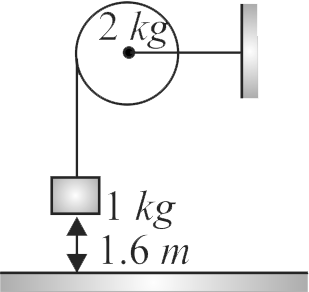

366266 Two rotating bodies \(A\) and \(B\) of masess \(m\) and \(2\;m\) with moments of inertia \({I_A}\) and \({I_B}\left( {{I_B} > {I_A}} \right)\) have equal kinetic energy of rotation. If \({L_A}\) and \({L_B}\) be their angular momentam respectively, then

366267 The ring of radius 1 \(m\) and mass 15 \(kg\) is rotating about its diameter with angular velocity of
25 rad/\(\sec \) Its kinetic energy is

366264 Moment of inertia of a body about given axis is \(2.4\;kg\;{m^2}\). Initially it is at rest. An angular acceleration of \(25\,rad/{s^2}\) is applied on it for \(t_{0}\) time so that its rotational kinetic energy becomes 1500 joule. The \(t_{o}\) is

366265 A body of mass \(1\,kg\) is suspended by a weightless string which passes over a frictionless pulley of mass \(2\,kg\) as shown in the figure. The mass is released from a height of \({1.6 m}\) from the ground. With what velocity does it strike the ground?

366266 Two rotating bodies \(A\) and \(B\) of masess \(m\) and \(2\;m\) with moments of inertia \({I_A}\) and \({I_B}\left( {{I_B} > {I_A}} \right)\) have equal kinetic energy of rotation. If \({L_A}\) and \({L_B}\) be their angular momentam respectively, then

366267 The ring of radius 1 \(m\) and mass 15 \(kg\) is rotating about its diameter with angular velocity of
25 rad/\(\sec \) Its kinetic energy is

366264 Moment of inertia of a body about given axis is \(2.4\;kg\;{m^2}\). Initially it is at rest. An angular acceleration of \(25\,rad/{s^2}\) is applied on it for \(t_{0}\) time so that its rotational kinetic energy becomes 1500 joule. The \(t_{o}\) is

366265 A body of mass \(1\,kg\) is suspended by a weightless string which passes over a frictionless pulley of mass \(2\,kg\) as shown in the figure. The mass is released from a height of \({1.6 m}\) from the ground. With what velocity does it strike the ground?

366266 Two rotating bodies \(A\) and \(B\) of masess \(m\) and \(2\;m\) with moments of inertia \({I_A}\) and \({I_B}\left( {{I_B} > {I_A}} \right)\) have equal kinetic energy of rotation. If \({L_A}\) and \({L_B}\) be their angular momentam respectively, then

366267 The ring of radius 1 \(m\) and mass 15 \(kg\) is rotating about its diameter with angular velocity of
25 rad/\(\sec \) Its kinetic energy is

366264 Moment of inertia of a body about given axis is \(2.4\;kg\;{m^2}\). Initially it is at rest. An angular acceleration of \(25\,rad/{s^2}\) is applied on it for \(t_{0}\) time so that its rotational kinetic energy becomes 1500 joule. The \(t_{o}\) is

366265 A body of mass \(1\,kg\) is suspended by a weightless string which passes over a frictionless pulley of mass \(2\,kg\) as shown in the figure. The mass is released from a height of \({1.6 m}\) from the ground. With what velocity does it strike the ground?

366266 Two rotating bodies \(A\) and \(B\) of masess \(m\) and \(2\;m\) with moments of inertia \({I_A}\) and \({I_B}\left( {{I_B} > {I_A}} \right)\) have equal kinetic energy of rotation. If \({L_A}\) and \({L_B}\) be their angular momentam respectively, then

366267 The ring of radius 1 \(m\) and mass 15 \(kg\) is rotating about its diameter with angular velocity of
25 rad/\(\sec \) Its kinetic energy is