366246 A solid sphere of mass \(\mathrm{m}\) and ratio \(R\) is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation \(\left( {{E_{{\rm{sphere }}}}/{E_{{\rm{cylinder }}}}} \right)\) will be

366247 If the angular momentum of a rotating body about a fixed axis is increased by \(10 \%\). Its kinetic energy will be increased by

366248 A rigid rod of length \({l}\) and negligible mass has a ball of mass \({m}\) attached to one end with its other end fixed, to form a pendulum as shown in figure. The pendulum is inverted, with the rod vertically up, and then released. Find the tension in the rod at the lowest point of the trajectory of ball.

366249 A rod of length \(L\) is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position is

366250 A ring and a disc of different masses are rotating with the same kinetic energy. If we apply a retarding torque \(\tau\) on the ring, it stops after completing \(n\) revolutions in all. If same torque is applied to the disc, how many revolutions would it complete in all before stopping?

366246 A solid sphere of mass \(\mathrm{m}\) and ratio \(R\) is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation \(\left( {{E_{{\rm{sphere }}}}/{E_{{\rm{cylinder }}}}} \right)\) will be

366247 If the angular momentum of a rotating body about a fixed axis is increased by \(10 \%\). Its kinetic energy will be increased by

366248 A rigid rod of length \({l}\) and negligible mass has a ball of mass \({m}\) attached to one end with its other end fixed, to form a pendulum as shown in figure. The pendulum is inverted, with the rod vertically up, and then released. Find the tension in the rod at the lowest point of the trajectory of ball.

366249 A rod of length \(L\) is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position is

366250 A ring and a disc of different masses are rotating with the same kinetic energy. If we apply a retarding torque \(\tau\) on the ring, it stops after completing \(n\) revolutions in all. If same torque is applied to the disc, how many revolutions would it complete in all before stopping?

366246 A solid sphere of mass \(\mathrm{m}\) and ratio \(R\) is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation \(\left( {{E_{{\rm{sphere }}}}/{E_{{\rm{cylinder }}}}} \right)\) will be

366247 If the angular momentum of a rotating body about a fixed axis is increased by \(10 \%\). Its kinetic energy will be increased by

366248 A rigid rod of length \({l}\) and negligible mass has a ball of mass \({m}\) attached to one end with its other end fixed, to form a pendulum as shown in figure. The pendulum is inverted, with the rod vertically up, and then released. Find the tension in the rod at the lowest point of the trajectory of ball.

366249 A rod of length \(L\) is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position is

366250 A ring and a disc of different masses are rotating with the same kinetic energy. If we apply a retarding torque \(\tau\) on the ring, it stops after completing \(n\) revolutions in all. If same torque is applied to the disc, how many revolutions would it complete in all before stopping?

366246 A solid sphere of mass \(\mathrm{m}\) and ratio \(R\) is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation \(\left( {{E_{{\rm{sphere }}}}/{E_{{\rm{cylinder }}}}} \right)\) will be

366247 If the angular momentum of a rotating body about a fixed axis is increased by \(10 \%\). Its kinetic energy will be increased by

366248 A rigid rod of length \({l}\) and negligible mass has a ball of mass \({m}\) attached to one end with its other end fixed, to form a pendulum as shown in figure. The pendulum is inverted, with the rod vertically up, and then released. Find the tension in the rod at the lowest point of the trajectory of ball.

366249 A rod of length \(L\) is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position is

366250 A ring and a disc of different masses are rotating with the same kinetic energy. If we apply a retarding torque \(\tau\) on the ring, it stops after completing \(n\) revolutions in all. If same torque is applied to the disc, how many revolutions would it complete in all before stopping?

366246 A solid sphere of mass \(\mathrm{m}\) and ratio \(R\) is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation \(\left( {{E_{{\rm{sphere }}}}/{E_{{\rm{cylinder }}}}} \right)\) will be

366247 If the angular momentum of a rotating body about a fixed axis is increased by \(10 \%\). Its kinetic energy will be increased by

366248 A rigid rod of length \({l}\) and negligible mass has a ball of mass \({m}\) attached to one end with its other end fixed, to form a pendulum as shown in figure. The pendulum is inverted, with the rod vertically up, and then released. Find the tension in the rod at the lowest point of the trajectory of ball.

366249 A rod of length \(L\) is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position is

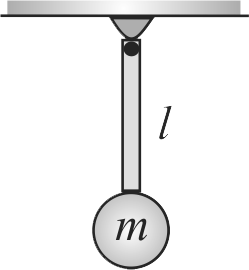
366250 A ring and a disc of different masses are rotating with the same kinetic energy. If we apply a retarding torque \(\tau\) on the ring, it stops after completing \(n\) revolutions in all. If same torque is applied to the disc, how many revolutions would it complete in all before stopping?