366202
A force \(F=2.0 \mathrm{~N}\) acts on a particle \(P\) in the \(x-z\) plane. The force \(F\) is parallel to \(X\)-axis. The particle \(P\) (as shown in the figure) is at a distance \(3\;m\) and the line joining \(P\) with the origin makes angle \(30^{\circ}\) with the \(X\)-axis. The magnitude of torque on \(P\) w.r.t. origin \(O\) (in \(N-m)\) is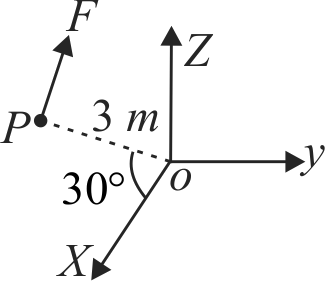
366203
\(A B C\) is an equilateral triangle with \(O\) as its centre. \(F_{1}, F_{2}\) and \(F_{3}\) represent three forces acting along the sides \(A B, B C\) and \(A C\), respectively. If the total torque about \(O\) is zero, then the magnitude of \(F_{3}\) is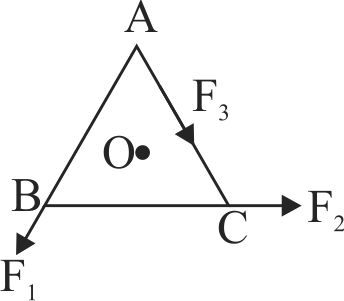
366202
A force \(F=2.0 \mathrm{~N}\) acts on a particle \(P\) in the \(x-z\) plane. The force \(F\) is parallel to \(X\)-axis. The particle \(P\) (as shown in the figure) is at a distance \(3\;m\) and the line joining \(P\) with the origin makes angle \(30^{\circ}\) with the \(X\)-axis. The magnitude of torque on \(P\) w.r.t. origin \(O\) (in \(N-m)\) is
366203
\(A B C\) is an equilateral triangle with \(O\) as its centre. \(F_{1}, F_{2}\) and \(F_{3}\) represent three forces acting along the sides \(A B, B C\) and \(A C\), respectively. If the total torque about \(O\) is zero, then the magnitude of \(F_{3}\) is
366202
A force \(F=2.0 \mathrm{~N}\) acts on a particle \(P\) in the \(x-z\) plane. The force \(F\) is parallel to \(X\)-axis. The particle \(P\) (as shown in the figure) is at a distance \(3\;m\) and the line joining \(P\) with the origin makes angle \(30^{\circ}\) with the \(X\)-axis. The magnitude of torque on \(P\) w.r.t. origin \(O\) (in \(N-m)\) is
366203
\(A B C\) is an equilateral triangle with \(O\) as its centre. \(F_{1}, F_{2}\) and \(F_{3}\) represent three forces acting along the sides \(A B, B C\) and \(A C\), respectively. If the total torque about \(O\) is zero, then the magnitude of \(F_{3}\) is
366202
A force \(F=2.0 \mathrm{~N}\) acts on a particle \(P\) in the \(x-z\) plane. The force \(F\) is parallel to \(X\)-axis. The particle \(P\) (as shown in the figure) is at a distance \(3\;m\) and the line joining \(P\) with the origin makes angle \(30^{\circ}\) with the \(X\)-axis. The magnitude of torque on \(P\) w.r.t. origin \(O\) (in \(N-m)\) is
366203
\(A B C\) is an equilateral triangle with \(O\) as its centre. \(F_{1}, F_{2}\) and \(F_{3}\) represent three forces acting along the sides \(A B, B C\) and \(A C\), respectively. If the total torque about \(O\) is zero, then the magnitude of \(F_{3}\) is