366075
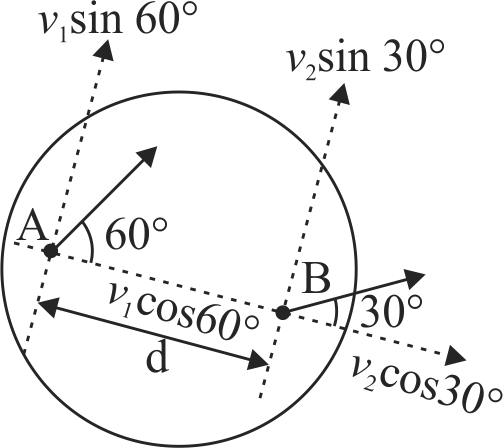
Two points \(A\) and \(B\) on a disc have velocities \(v_{1}\) and \(v_{2}\) respectively, at some moment. Their directions make angles \(60^{\circ}\) and \(30^{\circ}\), respectively, with the line of separation as shown in the figure. The angular velocity of disc is \((A\)and \(B\) are seperated by \('d'\))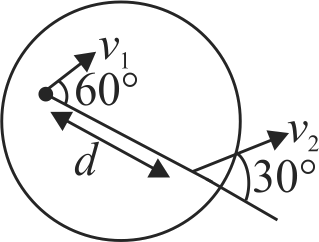
366077
Two particles \(A\) and \(B\) are situated at a distance \(d = 2\;m\) apart. Particle \(A\) has a velocity of \(10\;m/s\) at an angle of \(60^{\circ}\) and particle \(B\) has velocity \(v\) at an angle \(30^{\circ}\) as shown in the figure. The distance \(\mathrm{d}\) between \(A\) and \(B\) is constant. The angular velocity of \(B\) with respect to \(A\) is:
366075
Two points \(A\) and \(B\) on a disc have velocities \(v_{1}\) and \(v_{2}\) respectively, at some moment. Their directions make angles \(60^{\circ}\) and \(30^{\circ}\), respectively, with the line of separation as shown in the figure. The angular velocity of disc is \((A\)and \(B\) are seperated by \('d'\))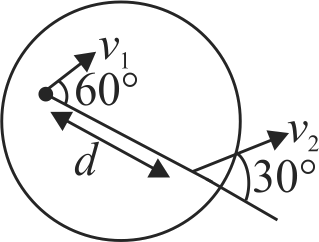
366077
Two particles \(A\) and \(B\) are situated at a distance \(d = 2\;m\) apart. Particle \(A\) has a velocity of \(10\;m/s\) at an angle of \(60^{\circ}\) and particle \(B\) has velocity \(v\) at an angle \(30^{\circ}\) as shown in the figure. The distance \(\mathrm{d}\) between \(A\) and \(B\) is constant. The angular velocity of \(B\) with respect to \(A\) is:
366075
Two points \(A\) and \(B\) on a disc have velocities \(v_{1}\) and \(v_{2}\) respectively, at some moment. Their directions make angles \(60^{\circ}\) and \(30^{\circ}\), respectively, with the line of separation as shown in the figure. The angular velocity of disc is \((A\)and \(B\) are seperated by \('d'\))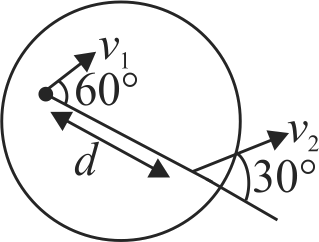
366077
Two particles \(A\) and \(B\) are situated at a distance \(d = 2\;m\) apart. Particle \(A\) has a velocity of \(10\;m/s\) at an angle of \(60^{\circ}\) and particle \(B\) has velocity \(v\) at an angle \(30^{\circ}\) as shown in the figure. The distance \(\mathrm{d}\) between \(A\) and \(B\) is constant. The angular velocity of \(B\) with respect to \(A\) is:
366075
Two points \(A\) and \(B\) on a disc have velocities \(v_{1}\) and \(v_{2}\) respectively, at some moment. Their directions make angles \(60^{\circ}\) and \(30^{\circ}\), respectively, with the line of separation as shown in the figure. The angular velocity of disc is \((A\)and \(B\) are seperated by \('d'\))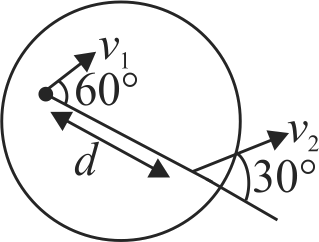
366077
Two particles \(A\) and \(B\) are situated at a distance \(d = 2\;m\) apart. Particle \(A\) has a velocity of \(10\;m/s\) at an angle of \(60^{\circ}\) and particle \(B\) has velocity \(v\) at an angle \(30^{\circ}\) as shown in the figure. The distance \(\mathrm{d}\) between \(A\) and \(B\) is constant. The angular velocity of \(B\) with respect to \(A\) is:
366075
Two points \(A\) and \(B\) on a disc have velocities \(v_{1}\) and \(v_{2}\) respectively, at some moment. Their directions make angles \(60^{\circ}\) and \(30^{\circ}\), respectively, with the line of separation as shown in the figure. The angular velocity of disc is \((A\)and \(B\) are seperated by \('d'\))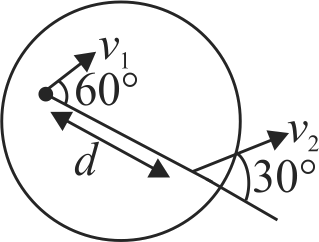
366077
Two particles \(A\) and \(B\) are situated at a distance \(d = 2\;m\) apart. Particle \(A\) has a velocity of \(10\;m/s\) at an angle of \(60^{\circ}\) and particle \(B\) has velocity \(v\) at an angle \(30^{\circ}\) as shown in the figure. The distance \(\mathrm{d}\) between \(A\) and \(B\) is constant. The angular velocity of \(B\) with respect to \(A\) is: