365842
A disc of radius \({r=0.1 {~m}}\) is rolled from a point \({A}\) on a track as shown in the figure. The part \({A B}\) of the track is a semi-circle of radius \({R}\) in a vertical plane. The disc rolls without sliding and leaves contact with the track at its highest point \({B}\). Flying through the air it strikes the ground at point \({C}\). The velocity of the centre of mass of the disc makes an angle of \({30^{\circ}}\) below the horizontal at the time of striking the ground. At the same instant, velocity of the topmost point \({P}\) of the disc is found to be \({6 {~m} / {s}}\). The value of \({R}\) (in \(m\)) (Take \({g=10 {~m} / {s}^{2}}\)) is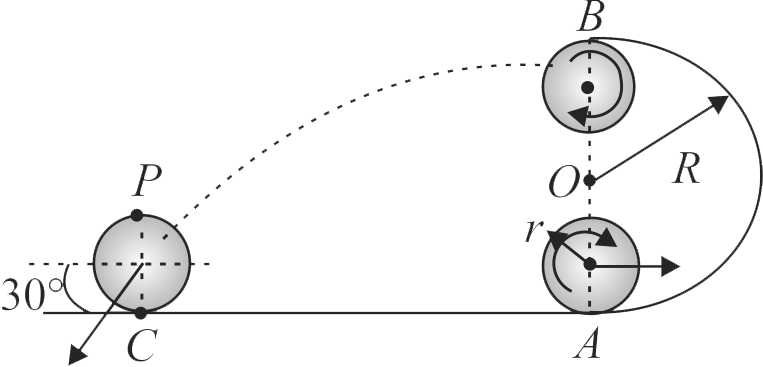
365842
A disc of radius \({r=0.1 {~m}}\) is rolled from a point \({A}\) on a track as shown in the figure. The part \({A B}\) of the track is a semi-circle of radius \({R}\) in a vertical plane. The disc rolls without sliding and leaves contact with the track at its highest point \({B}\). Flying through the air it strikes the ground at point \({C}\). The velocity of the centre of mass of the disc makes an angle of \({30^{\circ}}\) below the horizontal at the time of striking the ground. At the same instant, velocity of the topmost point \({P}\) of the disc is found to be \({6 {~m} / {s}}\). The value of \({R}\) (in \(m\)) (Take \({g=10 {~m} / {s}^{2}}\)) is
365842
A disc of radius \({r=0.1 {~m}}\) is rolled from a point \({A}\) on a track as shown in the figure. The part \({A B}\) of the track is a semi-circle of radius \({R}\) in a vertical plane. The disc rolls without sliding and leaves contact with the track at its highest point \({B}\). Flying through the air it strikes the ground at point \({C}\). The velocity of the centre of mass of the disc makes an angle of \({30^{\circ}}\) below the horizontal at the time of striking the ground. At the same instant, velocity of the topmost point \({P}\) of the disc is found to be \({6 {~m} / {s}}\). The value of \({R}\) (in \(m\)) (Take \({g=10 {~m} / {s}^{2}}\)) is
365842
A disc of radius \({r=0.1 {~m}}\) is rolled from a point \({A}\) on a track as shown in the figure. The part \({A B}\) of the track is a semi-circle of radius \({R}\) in a vertical plane. The disc rolls without sliding and leaves contact with the track at its highest point \({B}\). Flying through the air it strikes the ground at point \({C}\). The velocity of the centre of mass of the disc makes an angle of \({30^{\circ}}\) below the horizontal at the time of striking the ground. At the same instant, velocity of the topmost point \({P}\) of the disc is found to be \({6 {~m} / {s}}\). The value of \({R}\) (in \(m\)) (Take \({g=10 {~m} / {s}^{2}}\)) is
365842
A disc of radius \({r=0.1 {~m}}\) is rolled from a point \({A}\) on a track as shown in the figure. The part \({A B}\) of the track is a semi-circle of radius \({R}\) in a vertical plane. The disc rolls without sliding and leaves contact with the track at its highest point \({B}\). Flying through the air it strikes the ground at point \({C}\). The velocity of the centre of mass of the disc makes an angle of \({30^{\circ}}\) below the horizontal at the time of striking the ground. At the same instant, velocity of the topmost point \({P}\) of the disc is found to be \({6 {~m} / {s}}\). The value of \({R}\) (in \(m\)) (Take \({g=10 {~m} / {s}^{2}}\)) is