365810 A small bead of mass \(m\) moving with velocity \(v\) gets threaded on a stationary semicircular ring of mass \(m\) and radius \(R\) kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?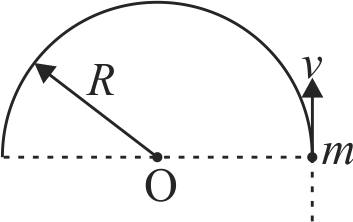

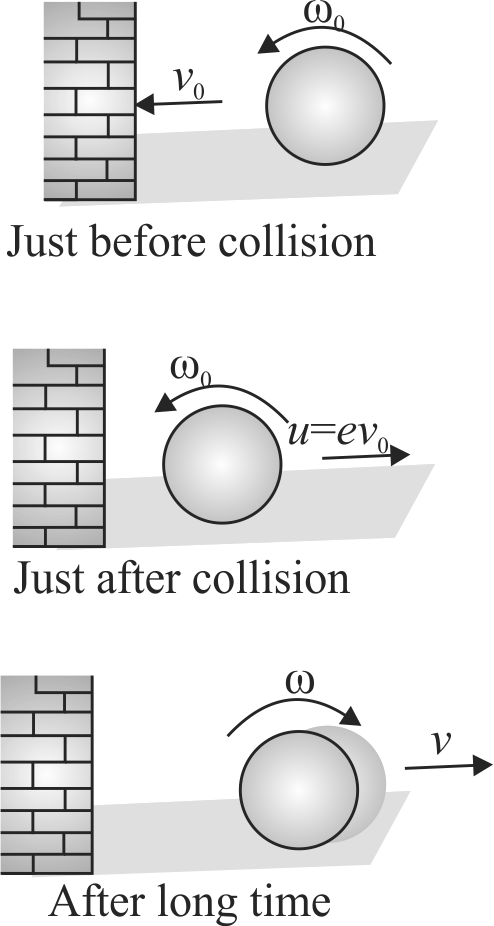
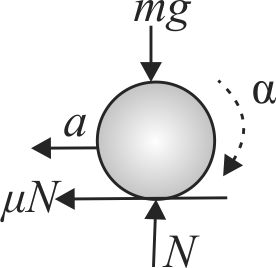
365811 A ball of radius \(R=20 {~cm}\) has mass \(m=0.75 {~kg}\) and moment of inertia (about its diameter) \(I=0.0125 {~kg} {~m}^{2}\). The ball rolls without sliding over a rough horizontal floor with velocity \({v_0} = 10\,\,m{s^{ - 1}}\) towards a smooth vertical wall.If coefficient of restitution between the wall and the ball is \(e=0.7\), calculate velocity \(v\) of the ball long after the collision (in \({m} / {s}\) ). (Take \(g=10 {~m} / {s}^{2}\) )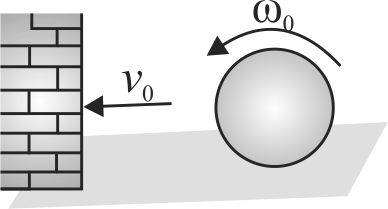

365812 A smooth sphere \(A\) is moving on a frictionless horizontal plane with angular speed \(\omega\) and centre of mass velocity \(v\). It collides elastically and head on with an identical sphere \(B\) at rest. Neglect friction everywhere. After the collision, their angular speeds are \({\omega _A}\) and \({\omega _B}\), respectively. Then

365813 A mass \(m\) is moving at speed \(v\) perpendicular to a rod of length \(d\) and mass \(M = 6\;m\) which pivots around a frictionless axle running through its centre. It strikes to the end of the rod. The moment of inertia of the rod about its centre is \(\dfrac{M d^{2}}{12}\). Then the angular speed of the system just after the collision is

365814 A block of mass \(m\) is attached to a pulley disc of equal mass \(m\) and radius \(r\) by means of a slack string as shown in figure. The pulley is hinged about its centre on a horizontal table and the block is projected with a initial velocity of \(5 \mathrm{~m} / \mathrm{s}\). The velocity of the block when the string becomes taut will be

365810 A small bead of mass \(m\) moving with velocity \(v\) gets threaded on a stationary semicircular ring of mass \(m\) and radius \(R\) kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?

365811 A ball of radius \(R=20 {~cm}\) has mass \(m=0.75 {~kg}\) and moment of inertia (about its diameter) \(I=0.0125 {~kg} {~m}^{2}\). The ball rolls without sliding over a rough horizontal floor with velocity \({v_0} = 10\,\,m{s^{ - 1}}\) towards a smooth vertical wall.If coefficient of restitution between the wall and the ball is \(e=0.7\), calculate velocity \(v\) of the ball long after the collision (in \({m} / {s}\) ). (Take \(g=10 {~m} / {s}^{2}\) )

365812 A smooth sphere \(A\) is moving on a frictionless horizontal plane with angular speed \(\omega\) and centre of mass velocity \(v\). It collides elastically and head on with an identical sphere \(B\) at rest. Neglect friction everywhere. After the collision, their angular speeds are \({\omega _A}\) and \({\omega _B}\), respectively. Then

365813 A mass \(m\) is moving at speed \(v\) perpendicular to a rod of length \(d\) and mass \(M = 6\;m\) which pivots around a frictionless axle running through its centre. It strikes to the end of the rod. The moment of inertia of the rod about its centre is \(\dfrac{M d^{2}}{12}\). Then the angular speed of the system just after the collision is

365814 A block of mass \(m\) is attached to a pulley disc of equal mass \(m\) and radius \(r\) by means of a slack string as shown in figure. The pulley is hinged about its centre on a horizontal table and the block is projected with a initial velocity of \(5 \mathrm{~m} / \mathrm{s}\). The velocity of the block when the string becomes taut will be

365810 A small bead of mass \(m\) moving with velocity \(v\) gets threaded on a stationary semicircular ring of mass \(m\) and radius \(R\) kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?

365811 A ball of radius \(R=20 {~cm}\) has mass \(m=0.75 {~kg}\) and moment of inertia (about its diameter) \(I=0.0125 {~kg} {~m}^{2}\). The ball rolls without sliding over a rough horizontal floor with velocity \({v_0} = 10\,\,m{s^{ - 1}}\) towards a smooth vertical wall.If coefficient of restitution between the wall and the ball is \(e=0.7\), calculate velocity \(v\) of the ball long after the collision (in \({m} / {s}\) ). (Take \(g=10 {~m} / {s}^{2}\) )

365812 A smooth sphere \(A\) is moving on a frictionless horizontal plane with angular speed \(\omega\) and centre of mass velocity \(v\). It collides elastically and head on with an identical sphere \(B\) at rest. Neglect friction everywhere. After the collision, their angular speeds are \({\omega _A}\) and \({\omega _B}\), respectively. Then

365813 A mass \(m\) is moving at speed \(v\) perpendicular to a rod of length \(d\) and mass \(M = 6\;m\) which pivots around a frictionless axle running through its centre. It strikes to the end of the rod. The moment of inertia of the rod about its centre is \(\dfrac{M d^{2}}{12}\). Then the angular speed of the system just after the collision is

365814 A block of mass \(m\) is attached to a pulley disc of equal mass \(m\) and radius \(r\) by means of a slack string as shown in figure. The pulley is hinged about its centre on a horizontal table and the block is projected with a initial velocity of \(5 \mathrm{~m} / \mathrm{s}\). The velocity of the block when the string becomes taut will be

365810 A small bead of mass \(m\) moving with velocity \(v\) gets threaded on a stationary semicircular ring of mass \(m\) and radius \(R\) kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?

365811 A ball of radius \(R=20 {~cm}\) has mass \(m=0.75 {~kg}\) and moment of inertia (about its diameter) \(I=0.0125 {~kg} {~m}^{2}\). The ball rolls without sliding over a rough horizontal floor with velocity \({v_0} = 10\,\,m{s^{ - 1}}\) towards a smooth vertical wall.If coefficient of restitution between the wall and the ball is \(e=0.7\), calculate velocity \(v\) of the ball long after the collision (in \({m} / {s}\) ). (Take \(g=10 {~m} / {s}^{2}\) )

365812 A smooth sphere \(A\) is moving on a frictionless horizontal plane with angular speed \(\omega\) and centre of mass velocity \(v\). It collides elastically and head on with an identical sphere \(B\) at rest. Neglect friction everywhere. After the collision, their angular speeds are \({\omega _A}\) and \({\omega _B}\), respectively. Then

365813 A mass \(m\) is moving at speed \(v\) perpendicular to a rod of length \(d\) and mass \(M = 6\;m\) which pivots around a frictionless axle running through its centre. It strikes to the end of the rod. The moment of inertia of the rod about its centre is \(\dfrac{M d^{2}}{12}\). Then the angular speed of the system just after the collision is

365814 A block of mass \(m\) is attached to a pulley disc of equal mass \(m\) and radius \(r\) by means of a slack string as shown in figure. The pulley is hinged about its centre on a horizontal table and the block is projected with a initial velocity of \(5 \mathrm{~m} / \mathrm{s}\). The velocity of the block when the string becomes taut will be

365810 A small bead of mass \(m\) moving with velocity \(v\) gets threaded on a stationary semicircular ring of mass \(m\) and radius \(R\) kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?

365811 A ball of radius \(R=20 {~cm}\) has mass \(m=0.75 {~kg}\) and moment of inertia (about its diameter) \(I=0.0125 {~kg} {~m}^{2}\). The ball rolls without sliding over a rough horizontal floor with velocity \({v_0} = 10\,\,m{s^{ - 1}}\) towards a smooth vertical wall.If coefficient of restitution between the wall and the ball is \(e=0.7\), calculate velocity \(v\) of the ball long after the collision (in \({m} / {s}\) ). (Take \(g=10 {~m} / {s}^{2}\) )

365812 A smooth sphere \(A\) is moving on a frictionless horizontal plane with angular speed \(\omega\) and centre of mass velocity \(v\). It collides elastically and head on with an identical sphere \(B\) at rest. Neglect friction everywhere. After the collision, their angular speeds are \({\omega _A}\) and \({\omega _B}\), respectively. Then

365813 A mass \(m\) is moving at speed \(v\) perpendicular to a rod of length \(d\) and mass \(M = 6\;m\) which pivots around a frictionless axle running through its centre. It strikes to the end of the rod. The moment of inertia of the rod about its centre is \(\dfrac{M d^{2}}{12}\). Then the angular speed of the system just after the collision is

365814 A block of mass \(m\) is attached to a pulley disc of equal mass \(m\) and radius \(r\) by means of a slack string as shown in figure. The pulley is hinged about its centre on a horizontal table and the block is projected with a initial velocity of \(5 \mathrm{~m} / \mathrm{s}\). The velocity of the block when the string becomes taut will be