365806
A small ball of mass \(m\) is projected with a minimum horizontal velocity \(v_{0}\) on a smooth wedge of mass \(M\) so that it will reach the highest point \(P\) of the wedge. If \(\dfrac{m}{M}=\dfrac{1}{4}\) and \(R=0.60 {~m}\), then find the value of \(v_{0}\). Take \(g=10 {~m} / {s}^{2}\).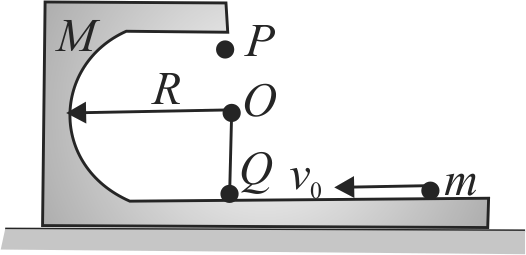
365807
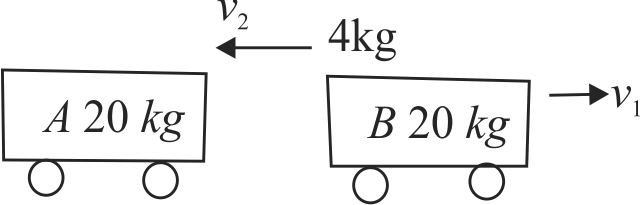
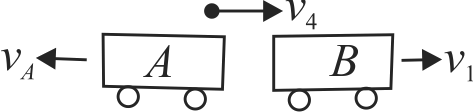
A child of mass 4 \(kg\) jumps from cart \(B\) to cart \(A\) and then immediately back to cart \(B\). The mass of each cart is 20 \(kg\) and they are initially at rest. In both the cases the child jumps at \(6 {~m} / {s}\) relative to the cart. If the cart moves along the same line with negligible friction with the final velocities of \(v_{B}\) and \(v_{A}\), respectively, find the ratio of \(6 v_{B}\) and \(5 v_{A}\).
365806
A small ball of mass \(m\) is projected with a minimum horizontal velocity \(v_{0}\) on a smooth wedge of mass \(M\) so that it will reach the highest point \(P\) of the wedge. If \(\dfrac{m}{M}=\dfrac{1}{4}\) and \(R=0.60 {~m}\), then find the value of \(v_{0}\). Take \(g=10 {~m} / {s}^{2}\).
365807
A child of mass 4 \(kg\) jumps from cart \(B\) to cart \(A\) and then immediately back to cart \(B\). The mass of each cart is 20 \(kg\) and they are initially at rest. In both the cases the child jumps at \(6 {~m} / {s}\) relative to the cart. If the cart moves along the same line with negligible friction with the final velocities of \(v_{B}\) and \(v_{A}\), respectively, find the ratio of \(6 v_{B}\) and \(5 v_{A}\).
365806
A small ball of mass \(m\) is projected with a minimum horizontal velocity \(v_{0}\) on a smooth wedge of mass \(M\) so that it will reach the highest point \(P\) of the wedge. If \(\dfrac{m}{M}=\dfrac{1}{4}\) and \(R=0.60 {~m}\), then find the value of \(v_{0}\). Take \(g=10 {~m} / {s}^{2}\).
365807
A child of mass 4 \(kg\) jumps from cart \(B\) to cart \(A\) and then immediately back to cart \(B\). The mass of each cart is 20 \(kg\) and they are initially at rest. In both the cases the child jumps at \(6 {~m} / {s}\) relative to the cart. If the cart moves along the same line with negligible friction with the final velocities of \(v_{B}\) and \(v_{A}\), respectively, find the ratio of \(6 v_{B}\) and \(5 v_{A}\).
365806
A small ball of mass \(m\) is projected with a minimum horizontal velocity \(v_{0}\) on a smooth wedge of mass \(M\) so that it will reach the highest point \(P\) of the wedge. If \(\dfrac{m}{M}=\dfrac{1}{4}\) and \(R=0.60 {~m}\), then find the value of \(v_{0}\). Take \(g=10 {~m} / {s}^{2}\).
365807
A child of mass 4 \(kg\) jumps from cart \(B\) to cart \(A\) and then immediately back to cart \(B\). The mass of each cart is 20 \(kg\) and they are initially at rest. In both the cases the child jumps at \(6 {~m} / {s}\) relative to the cart. If the cart moves along the same line with negligible friction with the final velocities of \(v_{B}\) and \(v_{A}\), respectively, find the ratio of \(6 v_{B}\) and \(5 v_{A}\).