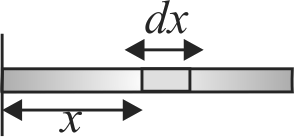
365758 The centre of mass of a non-uniform rod of length \(L\) whose mass per unit length \(\lambda\) varies as \(\lambda=\dfrac{k \cdot x^{2}}{L}\) where \(k\) is a constant and \(x\) is the distance of any point on rod from its one end, is (from the same end)

365759 A uniform thin \(\operatorname{rod} \mathrm{AB}\) of length \(\mathrm{L}\) has linear mass density \(\mu(x)=a+\dfrac{\mathrm{b} x}{\mathrm{~L}}\), where \(\mathrm{x}\) is measured from A. If the \(\mathrm{CM}\) of the rod lies at a distance of \(\left(\dfrac{7}{12}\right) \mathrm{L}\) from \(\mathrm{A}\), then \(a\) and \(\mathrm{b}\) are related as:

365760 Which of the following points is the likely position of the centre of mass of the system shown in figure.

365761 Assertion :
The centre of mass of a body may lie where there is no mass.
Reason :
Centre of mass of a body is a point, where the whole mass of the body is supposed to be concentrated.

365758 The centre of mass of a non-uniform rod of length \(L\) whose mass per unit length \(\lambda\) varies as \(\lambda=\dfrac{k \cdot x^{2}}{L}\) where \(k\) is a constant and \(x\) is the distance of any point on rod from its one end, is (from the same end)

365759 A uniform thin \(\operatorname{rod} \mathrm{AB}\) of length \(\mathrm{L}\) has linear mass density \(\mu(x)=a+\dfrac{\mathrm{b} x}{\mathrm{~L}}\), where \(\mathrm{x}\) is measured from A. If the \(\mathrm{CM}\) of the rod lies at a distance of \(\left(\dfrac{7}{12}\right) \mathrm{L}\) from \(\mathrm{A}\), then \(a\) and \(\mathrm{b}\) are related as:

365760 Which of the following points is the likely position of the centre of mass of the system shown in figure.

365761 Assertion :
The centre of mass of a body may lie where there is no mass.
Reason :
Centre of mass of a body is a point, where the whole mass of the body is supposed to be concentrated.

365758 The centre of mass of a non-uniform rod of length \(L\) whose mass per unit length \(\lambda\) varies as \(\lambda=\dfrac{k \cdot x^{2}}{L}\) where \(k\) is a constant and \(x\) is the distance of any point on rod from its one end, is (from the same end)

365759 A uniform thin \(\operatorname{rod} \mathrm{AB}\) of length \(\mathrm{L}\) has linear mass density \(\mu(x)=a+\dfrac{\mathrm{b} x}{\mathrm{~L}}\), where \(\mathrm{x}\) is measured from A. If the \(\mathrm{CM}\) of the rod lies at a distance of \(\left(\dfrac{7}{12}\right) \mathrm{L}\) from \(\mathrm{A}\), then \(a\) and \(\mathrm{b}\) are related as:

365760 Which of the following points is the likely position of the centre of mass of the system shown in figure.

365761 Assertion :
The centre of mass of a body may lie where there is no mass.
Reason :
Centre of mass of a body is a point, where the whole mass of the body is supposed to be concentrated.

365758 The centre of mass of a non-uniform rod of length \(L\) whose mass per unit length \(\lambda\) varies as \(\lambda=\dfrac{k \cdot x^{2}}{L}\) where \(k\) is a constant and \(x\) is the distance of any point on rod from its one end, is (from the same end)

365759 A uniform thin \(\operatorname{rod} \mathrm{AB}\) of length \(\mathrm{L}\) has linear mass density \(\mu(x)=a+\dfrac{\mathrm{b} x}{\mathrm{~L}}\), where \(\mathrm{x}\) is measured from A. If the \(\mathrm{CM}\) of the rod lies at a distance of \(\left(\dfrac{7}{12}\right) \mathrm{L}\) from \(\mathrm{A}\), then \(a\) and \(\mathrm{b}\) are related as:

365760 Which of the following points is the likely position of the centre of mass of the system shown in figure.

365761 Assertion :
The centre of mass of a body may lie where there is no mass.
Reason :
Centre of mass of a body is a point, where the whole mass of the body is supposed to be concentrated.