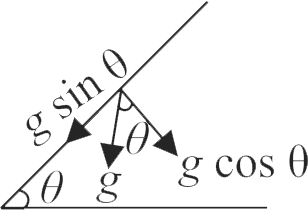365634 A spherical body of mass \({m}\) and radius \({r}\) is released from rest along a smooth inclined plane of inclination \({\theta}\). The angular momentum of the body about the instantaneous point of contact after a time ' \({t}\) ' from the instant of release is
365634 A spherical body of mass \({m}\) and radius \({r}\) is released from rest along a smooth inclined plane of inclination \({\theta}\). The angular momentum of the body about the instantaneous point of contact after a time ' \({t}\) ' from the instant of release is
365634 A spherical body of mass \({m}\) and radius \({r}\) is released from rest along a smooth inclined plane of inclination \({\theta}\). The angular momentum of the body about the instantaneous point of contact after a time ' \({t}\) ' from the instant of release is
365634 A spherical body of mass \({m}\) and radius \({r}\) is released from rest along a smooth inclined plane of inclination \({\theta}\). The angular momentum of the body about the instantaneous point of contact after a time ' \({t}\) ' from the instant of release is