365667 A girl is sitting on a weightless platform. Initially the girl is rotating about the vertical axis as shown in the figure. If frictional force is neglected and girl bends her hand, then

365668 The angular speed of a body changes from \(\omega_{1}\) and \(\omega_{2}\) without allowing a torque but due to change in its moment of inertia. The ratio of radii of gyration in the two cases is

365669 A disc of mass \(2\;kg\) and radius \(0.2\;m\) is rotating with angular velocity \(30{\kern 1pt} \,rad{s^{ - 1}}.\) What is angular velocity, if a mass of \(0.25\;kg\) is put on periphery of the disc?

365670 An ice skater starts a spin with her arms stretched out to the sides. She balances on the tip of one skate to turn without friction. She then pulls her arms in so that her moment of inertia decreases by a factor of 2 . In the process of her doing so, her kinetic energy becomes \({n}\) times the initial kinetic energy. Find the value of \({n}\) is

365667 A girl is sitting on a weightless platform. Initially the girl is rotating about the vertical axis as shown in the figure. If frictional force is neglected and girl bends her hand, then

365668 The angular speed of a body changes from \(\omega_{1}\) and \(\omega_{2}\) without allowing a torque but due to change in its moment of inertia. The ratio of radii of gyration in the two cases is

365669 A disc of mass \(2\;kg\) and radius \(0.2\;m\) is rotating with angular velocity \(30{\kern 1pt} \,rad{s^{ - 1}}.\) What is angular velocity, if a mass of \(0.25\;kg\) is put on periphery of the disc?

365670 An ice skater starts a spin with her arms stretched out to the sides. She balances on the tip of one skate to turn without friction. She then pulls her arms in so that her moment of inertia decreases by a factor of 2 . In the process of her doing so, her kinetic energy becomes \({n}\) times the initial kinetic energy. Find the value of \({n}\) is

365667 A girl is sitting on a weightless platform. Initially the girl is rotating about the vertical axis as shown in the figure. If frictional force is neglected and girl bends her hand, then

365668 The angular speed of a body changes from \(\omega_{1}\) and \(\omega_{2}\) without allowing a torque but due to change in its moment of inertia. The ratio of radii of gyration in the two cases is

365669 A disc of mass \(2\;kg\) and radius \(0.2\;m\) is rotating with angular velocity \(30{\kern 1pt} \,rad{s^{ - 1}}.\) What is angular velocity, if a mass of \(0.25\;kg\) is put on periphery of the disc?

365670 An ice skater starts a spin with her arms stretched out to the sides. She balances on the tip of one skate to turn without friction. She then pulls her arms in so that her moment of inertia decreases by a factor of 2 . In the process of her doing so, her kinetic energy becomes \({n}\) times the initial kinetic energy. Find the value of \({n}\) is

365667 A girl is sitting on a weightless platform. Initially the girl is rotating about the vertical axis as shown in the figure. If frictional force is neglected and girl bends her hand, then

365668 The angular speed of a body changes from \(\omega_{1}\) and \(\omega_{2}\) without allowing a torque but due to change in its moment of inertia. The ratio of radii of gyration in the two cases is

365669 A disc of mass \(2\;kg\) and radius \(0.2\;m\) is rotating with angular velocity \(30{\kern 1pt} \,rad{s^{ - 1}}.\) What is angular velocity, if a mass of \(0.25\;kg\) is put on periphery of the disc?

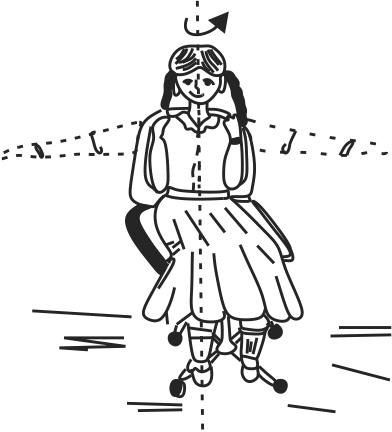
365670 An ice skater starts a spin with her arms stretched out to the sides. She balances on the tip of one skate to turn without friction. She then pulls her arms in so that her moment of inertia decreases by a factor of 2 . In the process of her doing so, her kinetic energy becomes \({n}\) times the initial kinetic energy. Find the value of \({n}\) is