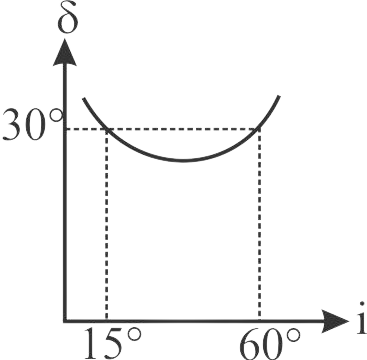
365060 The angle of incidence for a ray of light at a refracting surface of a prism is 45°. The angle of prism is 60°. If the ray suffers minimum deviation through the prism, the angle of minimum deviation and refractive index of the material of the prism respectively, are:
365060 The angle of incidence for a ray of light at a refracting surface of a prism is 45°. The angle of prism is 60°. If the ray suffers minimum deviation through the prism, the angle of minimum deviation and refractive index of the material of the prism respectively, are:
365060 The angle of incidence for a ray of light at a refracting surface of a prism is 45°. The angle of prism is 60°. If the ray suffers minimum deviation through the prism, the angle of minimum deviation and refractive index of the material of the prism respectively, are:
365060 The angle of incidence for a ray of light at a refracting surface of a prism is 45°. The angle of prism is 60°. If the ray suffers minimum deviation through the prism, the angle of minimum deviation and refractive index of the material of the prism respectively, are: