365101
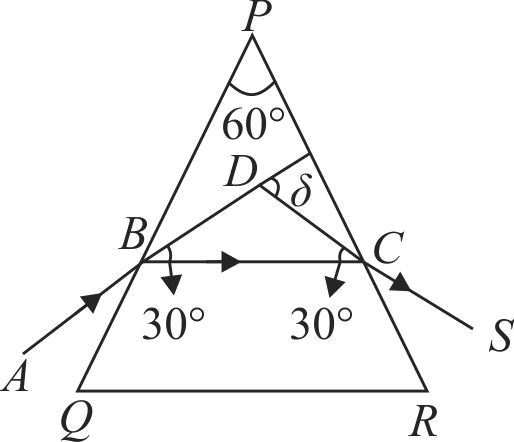
A ray \(P Q\) incident on the refracting face \(B A\) is refracted in the prism \(B A C\) as shown in the figure and emerges from the other refracting face \(A C\) as \(R S\), such that \(A Q=A R\). If the angle of prism \(A=60^{\circ}\) and the refractive index of the material of prism is \(\sqrt{3}\), then the angle of deviation of the ray is:
365102
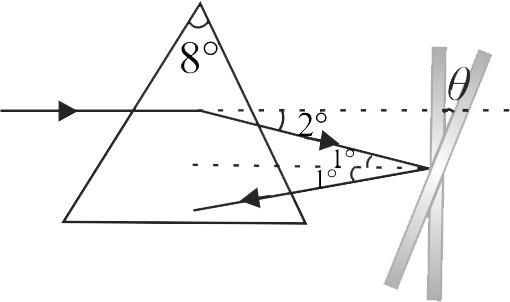
A horizontal ray is incident on one of the refracting faces of a prism of angle \(8^{\circ}\). The ray strikes a vertical plane mirror after refraction as shown in figure. Find the angle by which the mirror should be rotated in order to make the reflected ray antiparallel to incident ray.
(Take \(R.I.\) of material of prism \(=5 / 4\) )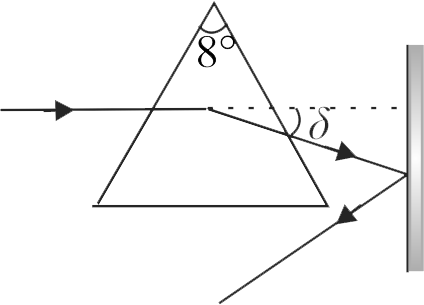
365101
A ray \(P Q\) incident on the refracting face \(B A\) is refracted in the prism \(B A C\) as shown in the figure and emerges from the other refracting face \(A C\) as \(R S\), such that \(A Q=A R\). If the angle of prism \(A=60^{\circ}\) and the refractive index of the material of prism is \(\sqrt{3}\), then the angle of deviation of the ray is:
365102
A horizontal ray is incident on one of the refracting faces of a prism of angle \(8^{\circ}\). The ray strikes a vertical plane mirror after refraction as shown in figure. Find the angle by which the mirror should be rotated in order to make the reflected ray antiparallel to incident ray.
(Take \(R.I.\) of material of prism \(=5 / 4\) )
365101
A ray \(P Q\) incident on the refracting face \(B A\) is refracted in the prism \(B A C\) as shown in the figure and emerges from the other refracting face \(A C\) as \(R S\), such that \(A Q=A R\). If the angle of prism \(A=60^{\circ}\) and the refractive index of the material of prism is \(\sqrt{3}\), then the angle of deviation of the ray is:
365102
A horizontal ray is incident on one of the refracting faces of a prism of angle \(8^{\circ}\). The ray strikes a vertical plane mirror after refraction as shown in figure. Find the angle by which the mirror should be rotated in order to make the reflected ray antiparallel to incident ray.
(Take \(R.I.\) of material of prism \(=5 / 4\) )
365101
A ray \(P Q\) incident on the refracting face \(B A\) is refracted in the prism \(B A C\) as shown in the figure and emerges from the other refracting face \(A C\) as \(R S\), such that \(A Q=A R\). If the angle of prism \(A=60^{\circ}\) and the refractive index of the material of prism is \(\sqrt{3}\), then the angle of deviation of the ray is:
365102
A horizontal ray is incident on one of the refracting faces of a prism of angle \(8^{\circ}\). The ray strikes a vertical plane mirror after refraction as shown in figure. Find the angle by which the mirror should be rotated in order to make the reflected ray antiparallel to incident ray.
(Take \(R.I.\) of material of prism \(=5 / 4\) )
365101
A ray \(P Q\) incident on the refracting face \(B A\) is refracted in the prism \(B A C\) as shown in the figure and emerges from the other refracting face \(A C\) as \(R S\), such that \(A Q=A R\). If the angle of prism \(A=60^{\circ}\) and the refractive index of the material of prism is \(\sqrt{3}\), then the angle of deviation of the ray is:
365102
A horizontal ray is incident on one of the refracting faces of a prism of angle \(8^{\circ}\). The ray strikes a vertical plane mirror after refraction as shown in figure. Find the angle by which the mirror should be rotated in order to make the reflected ray antiparallel to incident ray.
(Take \(R.I.\) of material of prism \(=5 / 4\) )