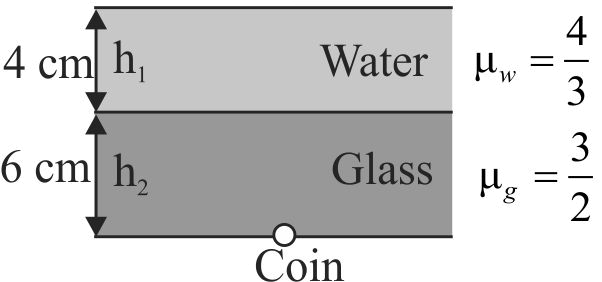
364896 A vessel of height \(2d\) is half filled with a liquid of refractive index \(\sqrt 2 \) and the other half with a liquid of refractive index \(n\).(The given liquids are immiscible). Then the apparent depth of the inner surface of the bottom of the vessel (neglecting the thickness of the bottom of the vessel) will be
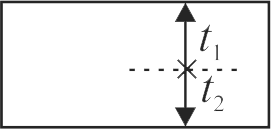
364897 \({\rm{P}}\) is a point on the axis of a concave mirror. The image of \({\rm{P}}\) formed by the mirror, coincides with \({\rm{P}}\). A rectangular glass slab of thickness \({\rm{t }}\) and refractive index \(\mu \) is now introduced between \({\rm{P}}\) and the mirror. For image of \({\rm{P}}\) to coincide with \({\rm{P}}\) again, the mirror must be moved
364896 A vessel of height \(2d\) is half filled with a liquid of refractive index \(\sqrt 2 \) and the other half with a liquid of refractive index \(n\).(The given liquids are immiscible). Then the apparent depth of the inner surface of the bottom of the vessel (neglecting the thickness of the bottom of the vessel) will be
364897 \({\rm{P}}\) is a point on the axis of a concave mirror. The image of \({\rm{P}}\) formed by the mirror, coincides with \({\rm{P}}\). A rectangular glass slab of thickness \({\rm{t }}\) and refractive index \(\mu \) is now introduced between \({\rm{P}}\) and the mirror. For image of \({\rm{P}}\) to coincide with \({\rm{P}}\) again, the mirror must be moved
364896 A vessel of height \(2d\) is half filled with a liquid of refractive index \(\sqrt 2 \) and the other half with a liquid of refractive index \(n\).(The given liquids are immiscible). Then the apparent depth of the inner surface of the bottom of the vessel (neglecting the thickness of the bottom of the vessel) will be
364897 \({\rm{P}}\) is a point on the axis of a concave mirror. The image of \({\rm{P}}\) formed by the mirror, coincides with \({\rm{P}}\). A rectangular glass slab of thickness \({\rm{t }}\) and refractive index \(\mu \) is now introduced between \({\rm{P}}\) and the mirror. For image of \({\rm{P}}\) to coincide with \({\rm{P}}\) again, the mirror must be moved
364896 A vessel of height \(2d\) is half filled with a liquid of refractive index \(\sqrt 2 \) and the other half with a liquid of refractive index \(n\).(The given liquids are immiscible). Then the apparent depth of the inner surface of the bottom of the vessel (neglecting the thickness of the bottom of the vessel) will be
364897 \({\rm{P}}\) is a point on the axis of a concave mirror. The image of \({\rm{P}}\) formed by the mirror, coincides with \({\rm{P}}\). A rectangular glass slab of thickness \({\rm{t }}\) and refractive index \(\mu \) is now introduced between \({\rm{P}}\) and the mirror. For image of \({\rm{P}}\) to coincide with \({\rm{P}}\) again, the mirror must be moved
364896 A vessel of height \(2d\) is half filled with a liquid of refractive index \(\sqrt 2 \) and the other half with a liquid of refractive index \(n\).(The given liquids are immiscible). Then the apparent depth of the inner surface of the bottom of the vessel (neglecting the thickness of the bottom of the vessel) will be
364897 \({\rm{P}}\) is a point on the axis of a concave mirror. The image of \({\rm{P}}\) formed by the mirror, coincides with \({\rm{P}}\). A rectangular glass slab of thickness \({\rm{t }}\) and refractive index \(\mu \) is now introduced between \({\rm{P}}\) and the mirror. For image of \({\rm{P}}\) to coincide with \({\rm{P}}\) again, the mirror must be moved