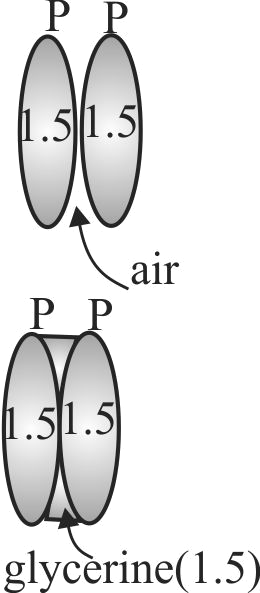
364765 Two similar thin equi-convex lenses, of focal length \(f\) each, are kept coaxially in contact with each other such that the focal length of the combination is \({F_1}\). When the space between the two lenses is filled with glycerine (which has the same refractive index (\(\mu = 1.5\)) as that of glass) then the equivalent focal length is \({F_2}\). The ratio \({F_1}:{F_2}\) will be :

364766 Two similar plano convex lenses are combined together in three different ways as shown in the adjoining figure. The ratio of the focal lengths in three cases will be

364767 A layered lens as shown in figure is made of two types of transparent materials indicated by different shades. A point object is placed on its axis. The object will form

364768 An equiconvex lens of radius of curvature \(14\,cm\) is made up of two different materials. Left half and right half of vertical portion is made up of material of refractive index 1.5 and 1.2 respectively as shown in the figure. If a point object is placed at a distance of \(40\,cm\), calculate the image distance.

364765 Two similar thin equi-convex lenses, of focal length \(f\) each, are kept coaxially in contact with each other such that the focal length of the combination is \({F_1}\). When the space between the two lenses is filled with glycerine (which has the same refractive index (\(\mu = 1.5\)) as that of glass) then the equivalent focal length is \({F_2}\). The ratio \({F_1}:{F_2}\) will be :

364766 Two similar plano convex lenses are combined together in three different ways as shown in the adjoining figure. The ratio of the focal lengths in three cases will be

364767 A layered lens as shown in figure is made of two types of transparent materials indicated by different shades. A point object is placed on its axis. The object will form

364768 An equiconvex lens of radius of curvature \(14\,cm\) is made up of two different materials. Left half and right half of vertical portion is made up of material of refractive index 1.5 and 1.2 respectively as shown in the figure. If a point object is placed at a distance of \(40\,cm\), calculate the image distance.

364765 Two similar thin equi-convex lenses, of focal length \(f\) each, are kept coaxially in contact with each other such that the focal length of the combination is \({F_1}\). When the space between the two lenses is filled with glycerine (which has the same refractive index (\(\mu = 1.5\)) as that of glass) then the equivalent focal length is \({F_2}\). The ratio \({F_1}:{F_2}\) will be :

364766 Two similar plano convex lenses are combined together in three different ways as shown in the adjoining figure. The ratio of the focal lengths in three cases will be

364767 A layered lens as shown in figure is made of two types of transparent materials indicated by different shades. A point object is placed on its axis. The object will form

364768 An equiconvex lens of radius of curvature \(14\,cm\) is made up of two different materials. Left half and right half of vertical portion is made up of material of refractive index 1.5 and 1.2 respectively as shown in the figure. If a point object is placed at a distance of \(40\,cm\), calculate the image distance.

364765 Two similar thin equi-convex lenses, of focal length \(f\) each, are kept coaxially in contact with each other such that the focal length of the combination is \({F_1}\). When the space between the two lenses is filled with glycerine (which has the same refractive index (\(\mu = 1.5\)) as that of glass) then the equivalent focal length is \({F_2}\). The ratio \({F_1}:{F_2}\) will be :

364766 Two similar plano convex lenses are combined together in three different ways as shown in the adjoining figure. The ratio of the focal lengths in three cases will be

364767 A layered lens as shown in figure is made of two types of transparent materials indicated by different shades. A point object is placed on its axis. The object will form

364768 An equiconvex lens of radius of curvature \(14\,cm\) is made up of two different materials. Left half and right half of vertical portion is made up of material of refractive index 1.5 and 1.2 respectively as shown in the figure. If a point object is placed at a distance of \(40\,cm\), calculate the image distance.