364753 Two thin biconvex lens have focal lengths \({f_1}\) and \({f_2}\) . A third thin biconcave lens has focal length of \({f_3}\). If the first two biconvex lenses are in contact, the total power of the lenses is \({P_1}\) . If the first convex lens is in contact with the third lens, the total power is \({P_2}\) . If the second lens is in contact with the third lens, the total power is \({P_3}\) then
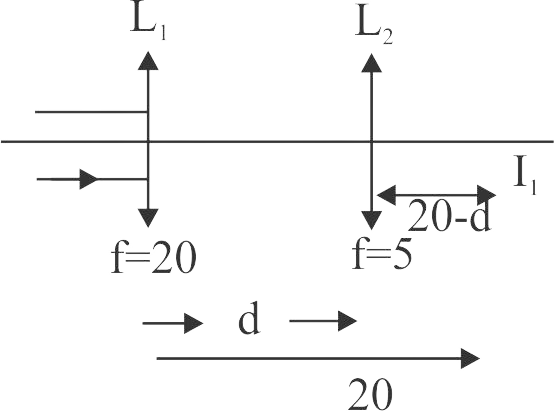
364754 A convex lens ‘\(A\)’ of focal length \(20\;cm\) and a concave lens ‘\(B\)’ of focal length \(5\;cm\) are kept along the same axis with a distance ‘\(d\)’ between them. If a parallel beam of light falling-on ‘\(A\)’ leaves ‘\(B\)’ as a parallel beam, then the distance ‘\(d\)’ in cm will be
364753 Two thin biconvex lens have focal lengths \({f_1}\) and \({f_2}\) . A third thin biconcave lens has focal length of \({f_3}\). If the first two biconvex lenses are in contact, the total power of the lenses is \({P_1}\) . If the first convex lens is in contact with the third lens, the total power is \({P_2}\) . If the second lens is in contact with the third lens, the total power is \({P_3}\) then
364754 A convex lens ‘\(A\)’ of focal length \(20\;cm\) and a concave lens ‘\(B\)’ of focal length \(5\;cm\) are kept along the same axis with a distance ‘\(d\)’ between them. If a parallel beam of light falling-on ‘\(A\)’ leaves ‘\(B\)’ as a parallel beam, then the distance ‘\(d\)’ in cm will be
364753 Two thin biconvex lens have focal lengths \({f_1}\) and \({f_2}\) . A third thin biconcave lens has focal length of \({f_3}\). If the first two biconvex lenses are in contact, the total power of the lenses is \({P_1}\) . If the first convex lens is in contact with the third lens, the total power is \({P_2}\) . If the second lens is in contact with the third lens, the total power is \({P_3}\) then
364754 A convex lens ‘\(A\)’ of focal length \(20\;cm\) and a concave lens ‘\(B\)’ of focal length \(5\;cm\) are kept along the same axis with a distance ‘\(d\)’ between them. If a parallel beam of light falling-on ‘\(A\)’ leaves ‘\(B\)’ as a parallel beam, then the distance ‘\(d\)’ in cm will be
364753 Two thin biconvex lens have focal lengths \({f_1}\) and \({f_2}\) . A third thin biconcave lens has focal length of \({f_3}\). If the first two biconvex lenses are in contact, the total power of the lenses is \({P_1}\) . If the first convex lens is in contact with the third lens, the total power is \({P_2}\) . If the second lens is in contact with the third lens, the total power is \({P_3}\) then
364754 A convex lens ‘\(A\)’ of focal length \(20\;cm\) and a concave lens ‘\(B\)’ of focal length \(5\;cm\) are kept along the same axis with a distance ‘\(d\)’ between them. If a parallel beam of light falling-on ‘\(A\)’ leaves ‘\(B\)’ as a parallel beam, then the distance ‘\(d\)’ in cm will be