364472
A pendulum has time period \(T\) for small oscillations. An obstacle is placed directly beneath the pivot, so that only the lowest one quarter of the string can follow the pendulum bob when it swings in the left of its resting position as shown in figure. The pendulum is released from rest at a certain point \(A\). The time taken by it to return to the point \(A\) is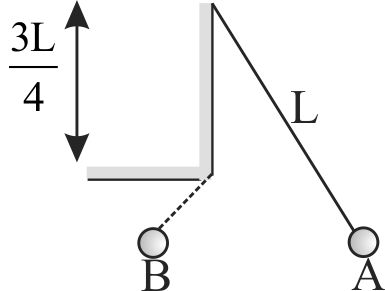
364472
A pendulum has time period \(T\) for small oscillations. An obstacle is placed directly beneath the pivot, so that only the lowest one quarter of the string can follow the pendulum bob when it swings in the left of its resting position as shown in figure. The pendulum is released from rest at a certain point \(A\). The time taken by it to return to the point \(A\) is
364472
A pendulum has time period \(T\) for small oscillations. An obstacle is placed directly beneath the pivot, so that only the lowest one quarter of the string can follow the pendulum bob when it swings in the left of its resting position as shown in figure. The pendulum is released from rest at a certain point \(A\). The time taken by it to return to the point \(A\) is
364472
A pendulum has time period \(T\) for small oscillations. An obstacle is placed directly beneath the pivot, so that only the lowest one quarter of the string can follow the pendulum bob when it swings in the left of its resting position as shown in figure. The pendulum is released from rest at a certain point \(A\). The time taken by it to return to the point \(A\) is
