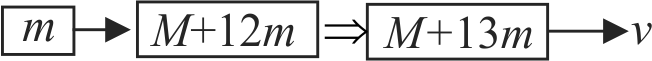364093
An oscillator of mass \(M\) is at rest in the equillibrium position in a potential
\(V=\dfrac{1}{2} k(x-X)^{2}\). A particle of mass \(m\) comes from right with speed \(u\) and collides completely inelastically with \(M\) and sticks to it. This process repeats every time the oscillator crosses its equillibrium position. The amplitude of oscillations after 13 collisions is:\((M=10, m=5, u=1, k=1)\)
364093
An oscillator of mass \(M\) is at rest in the equillibrium position in a potential
\(V=\dfrac{1}{2} k(x-X)^{2}\). A particle of mass \(m\) comes from right with speed \(u\) and collides completely inelastically with \(M\) and sticks to it. This process repeats every time the oscillator crosses its equillibrium position. The amplitude of oscillations after 13 collisions is:\((M=10, m=5, u=1, k=1)\)
364093
An oscillator of mass \(M\) is at rest in the equillibrium position in a potential
\(V=\dfrac{1}{2} k(x-X)^{2}\). A particle of mass \(m\) comes from right with speed \(u\) and collides completely inelastically with \(M\) and sticks to it. This process repeats every time the oscillator crosses its equillibrium position. The amplitude of oscillations after 13 collisions is:\((M=10, m=5, u=1, k=1)\)
364093
An oscillator of mass \(M\) is at rest in the equillibrium position in a potential
\(V=\dfrac{1}{2} k(x-X)^{2}\). A particle of mass \(m\) comes from right with speed \(u\) and collides completely inelastically with \(M\) and sticks to it. This process repeats every time the oscillator crosses its equillibrium position. The amplitude of oscillations after 13 collisions is:\((M=10, m=5, u=1, k=1)\)