358722 A square wire loop of \(10.0 \,cm\) side lies at right angles to a uniform magnetic field of \(7\,T\). A \(10\,V\) light bulb is in a series with the loop as shown in the figure. The magnetic field is decreasing steadily to zero over a time interval \({\Delta t}\). For what value of \({\Delta t}\), the bulb will shine with full brightness?

358723 A coil of 1200 turns and mean area of \(500\;\,c{m^2}\) is held perpendicular to a uniform magnetic field of induction \(4 \times {10^{ - 4}}\;T\). The resistance of the coil is \(20 \Omega\). When the coil is rotated through \(180^{\circ}\) in the magnetic field in \(0.1\;\,s,\) the average electric current (in \(mA\) ) induced is

358724 A big circular coil of 1000 turns and average radius \(10\;m\) is rotating about its horizontal diameter at \(2\,rad{s^{ - 1}}\). If the vertical component of earth's magnetic field at that place is
\(2 \times {10^{ - 5}}\;T\) and electrical resistance of the coil is \(12.56 \Omega\), then the maximum induced current in the coil will be

358725 A square wire loop with side \({L=1.0 {~m}}\) sides is perpendicular to a uniform magnetic field, with half the area of the loop in the field as shown in the figure. The resistance of the loop is \({35 \Omega}\) and the loop contains an ideal battery with emf \({\varepsilon=6.0 {~V}}\). If the magnitude of the field varies with time according to \({B=5.0-2.0 t}\), with \({B}\) in tesla and \({t}\) in seconds, what is the magnitude of the (net) current (in \(A\)) around the loop?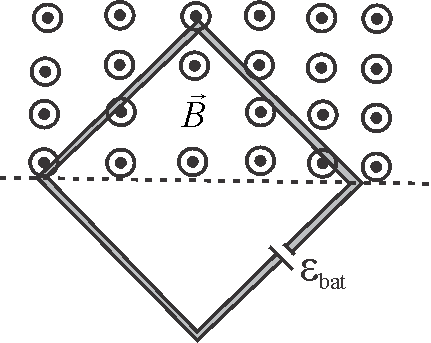

358726 The magnetic flux through a coil perpendicular to its plane is varying according to the relation \(\phi=\left(t^{3}+t^{2}+t-6\right) {Wb}\). If the resistance of the coil is \(5 \Omega\), calculate the induced current through the coil at \(t = 2\,s\) ?

358722 A square wire loop of \(10.0 \,cm\) side lies at right angles to a uniform magnetic field of \(7\,T\). A \(10\,V\) light bulb is in a series with the loop as shown in the figure. The magnetic field is decreasing steadily to zero over a time interval \({\Delta t}\). For what value of \({\Delta t}\), the bulb will shine with full brightness?

358723 A coil of 1200 turns and mean area of \(500\;\,c{m^2}\) is held perpendicular to a uniform magnetic field of induction \(4 \times {10^{ - 4}}\;T\). The resistance of the coil is \(20 \Omega\). When the coil is rotated through \(180^{\circ}\) in the magnetic field in \(0.1\;\,s,\) the average electric current (in \(mA\) ) induced is

358724 A big circular coil of 1000 turns and average radius \(10\;m\) is rotating about its horizontal diameter at \(2\,rad{s^{ - 1}}\). If the vertical component of earth's magnetic field at that place is
\(2 \times {10^{ - 5}}\;T\) and electrical resistance of the coil is \(12.56 \Omega\), then the maximum induced current in the coil will be

358725 A square wire loop with side \({L=1.0 {~m}}\) sides is perpendicular to a uniform magnetic field, with half the area of the loop in the field as shown in the figure. The resistance of the loop is \({35 \Omega}\) and the loop contains an ideal battery with emf \({\varepsilon=6.0 {~V}}\). If the magnitude of the field varies with time according to \({B=5.0-2.0 t}\), with \({B}\) in tesla and \({t}\) in seconds, what is the magnitude of the (net) current (in \(A\)) around the loop?

358726 The magnetic flux through a coil perpendicular to its plane is varying according to the relation \(\phi=\left(t^{3}+t^{2}+t-6\right) {Wb}\). If the resistance of the coil is \(5 \Omega\), calculate the induced current through the coil at \(t = 2\,s\) ?

358722 A square wire loop of \(10.0 \,cm\) side lies at right angles to a uniform magnetic field of \(7\,T\). A \(10\,V\) light bulb is in a series with the loop as shown in the figure. The magnetic field is decreasing steadily to zero over a time interval \({\Delta t}\). For what value of \({\Delta t}\), the bulb will shine with full brightness?

358723 A coil of 1200 turns and mean area of \(500\;\,c{m^2}\) is held perpendicular to a uniform magnetic field of induction \(4 \times {10^{ - 4}}\;T\). The resistance of the coil is \(20 \Omega\). When the coil is rotated through \(180^{\circ}\) in the magnetic field in \(0.1\;\,s,\) the average electric current (in \(mA\) ) induced is

358724 A big circular coil of 1000 turns and average radius \(10\;m\) is rotating about its horizontal diameter at \(2\,rad{s^{ - 1}}\). If the vertical component of earth's magnetic field at that place is
\(2 \times {10^{ - 5}}\;T\) and electrical resistance of the coil is \(12.56 \Omega\), then the maximum induced current in the coil will be

358725 A square wire loop with side \({L=1.0 {~m}}\) sides is perpendicular to a uniform magnetic field, with half the area of the loop in the field as shown in the figure. The resistance of the loop is \({35 \Omega}\) and the loop contains an ideal battery with emf \({\varepsilon=6.0 {~V}}\). If the magnitude of the field varies with time according to \({B=5.0-2.0 t}\), with \({B}\) in tesla and \({t}\) in seconds, what is the magnitude of the (net) current (in \(A\)) around the loop?

358726 The magnetic flux through a coil perpendicular to its plane is varying according to the relation \(\phi=\left(t^{3}+t^{2}+t-6\right) {Wb}\). If the resistance of the coil is \(5 \Omega\), calculate the induced current through the coil at \(t = 2\,s\) ?

358722 A square wire loop of \(10.0 \,cm\) side lies at right angles to a uniform magnetic field of \(7\,T\). A \(10\,V\) light bulb is in a series with the loop as shown in the figure. The magnetic field is decreasing steadily to zero over a time interval \({\Delta t}\). For what value of \({\Delta t}\), the bulb will shine with full brightness?

358723 A coil of 1200 turns and mean area of \(500\;\,c{m^2}\) is held perpendicular to a uniform magnetic field of induction \(4 \times {10^{ - 4}}\;T\). The resistance of the coil is \(20 \Omega\). When the coil is rotated through \(180^{\circ}\) in the magnetic field in \(0.1\;\,s,\) the average electric current (in \(mA\) ) induced is

358724 A big circular coil of 1000 turns and average radius \(10\;m\) is rotating about its horizontal diameter at \(2\,rad{s^{ - 1}}\). If the vertical component of earth's magnetic field at that place is
\(2 \times {10^{ - 5}}\;T\) and electrical resistance of the coil is \(12.56 \Omega\), then the maximum induced current in the coil will be

358725 A square wire loop with side \({L=1.0 {~m}}\) sides is perpendicular to a uniform magnetic field, with half the area of the loop in the field as shown in the figure. The resistance of the loop is \({35 \Omega}\) and the loop contains an ideal battery with emf \({\varepsilon=6.0 {~V}}\). If the magnitude of the field varies with time according to \({B=5.0-2.0 t}\), with \({B}\) in tesla and \({t}\) in seconds, what is the magnitude of the (net) current (in \(A\)) around the loop?

358726 The magnetic flux through a coil perpendicular to its plane is varying according to the relation \(\phi=\left(t^{3}+t^{2}+t-6\right) {Wb}\). If the resistance of the coil is \(5 \Omega\), calculate the induced current through the coil at \(t = 2\,s\) ?

358722 A square wire loop of \(10.0 \,cm\) side lies at right angles to a uniform magnetic field of \(7\,T\). A \(10\,V\) light bulb is in a series with the loop as shown in the figure. The magnetic field is decreasing steadily to zero over a time interval \({\Delta t}\). For what value of \({\Delta t}\), the bulb will shine with full brightness?

358723 A coil of 1200 turns and mean area of \(500\;\,c{m^2}\) is held perpendicular to a uniform magnetic field of induction \(4 \times {10^{ - 4}}\;T\). The resistance of the coil is \(20 \Omega\). When the coil is rotated through \(180^{\circ}\) in the magnetic field in \(0.1\;\,s,\) the average electric current (in \(mA\) ) induced is

358724 A big circular coil of 1000 turns and average radius \(10\;m\) is rotating about its horizontal diameter at \(2\,rad{s^{ - 1}}\). If the vertical component of earth's magnetic field at that place is
\(2 \times {10^{ - 5}}\;T\) and electrical resistance of the coil is \(12.56 \Omega\), then the maximum induced current in the coil will be

358725 A square wire loop with side \({L=1.0 {~m}}\) sides is perpendicular to a uniform magnetic field, with half the area of the loop in the field as shown in the figure. The resistance of the loop is \({35 \Omega}\) and the loop contains an ideal battery with emf \({\varepsilon=6.0 {~V}}\). If the magnitude of the field varies with time according to \({B=5.0-2.0 t}\), with \({B}\) in tesla and \({t}\) in seconds, what is the magnitude of the (net) current (in \(A\)) around the loop?

358726 The magnetic flux through a coil perpendicular to its plane is varying according to the relation \(\phi=\left(t^{3}+t^{2}+t-6\right) {Wb}\). If the resistance of the coil is \(5 \Omega\), calculate the induced current through the coil at \(t = 2\,s\) ?