Explanation:
Now, field at centre of outer square
\(B = \frac{{2\sqrt 2 {\mu _0}I}}{{\pi L}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Where current in the square loop is I.
Flux with small loop \((\phi)=B \cdot \pi R^{2}\)
\(\phi=\dfrac{2 \sqrt{2} \mu_{0} I}{\pi L} \cdot \pi R^{2}\)
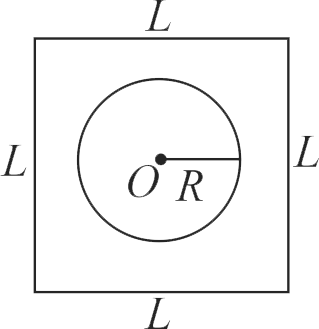
\(\phi = \frac{{2\sqrt 2 {\mu _0}I{R^2}}}{L}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
Now, mutual induction, \(M=\dfrac{\phi}{I}\)
\(M=\dfrac{2 \sqrt{2} \mu_{0} I R^{2}}{L I} \Rightarrow M=\dfrac{2 \sqrt{2} \mu_{0} R^{2}}{L}\)