358431 A \(0.1\;m\) long conductor carrying a current of 50 \(A\) is held perpendicular to a magnetic field of \(1.25\,mT\). The mechanical power required to move the conductor with a speed of \(1\;m{s^{ - 1}}\) is

358432 The figure shows a square loop \({L}\) of side \(5 {~cm}\) which is connected to a network of resistances. The whole setup is moving towards right with a constant speed of \(1 {cms}^{-1}\). At some instant, a part of \(L\) is in a uniform magnetic field of \(1 T\), perpendicular to the plane of loop. If the resistance of \(L\) is \(2.7 \,\Omega\), the current in the loop at that instant is found out to be \({N} \times 10^{-4} {~A}\)
\(\text { Find N. }\left[\text { Take } \dfrac{4}{3}=1.3\right]\)

358433 A circular loop of radius \(r\) is moved with a velocity \(v\) as shown in the diagram. The work needed to maintain its velocity constant is :

358434 A wire of length \(1\;m\) is moving at a speed of 2 \(m{s^{ - 1}}\) perpendicular to its length and a homogeneous magnetic field of \(0.5\;T\). The ends of the wire are joined to a circuit of resistance \(6 \Omega\). The rate at which work is being done to keep the wire moving at constant speed is:

358435 A square loop of area \(25\;c{m^2}\) has a resistance of \(10 \Omega\). The loop is placed in uniform magnetic field of magnitude \(40.0\,T.\) The plane of loop is perpendicular to the magnetic field. The work done in pulling the loop out of the magnetic field slowly and uniformly in \(1.0\,\sec ,\) will be

358431 A \(0.1\;m\) long conductor carrying a current of 50 \(A\) is held perpendicular to a magnetic field of \(1.25\,mT\). The mechanical power required to move the conductor with a speed of \(1\;m{s^{ - 1}}\) is

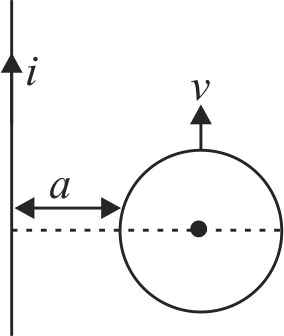
358432 The figure shows a square loop \({L}\) of side \(5 {~cm}\) which is connected to a network of resistances. The whole setup is moving towards right with a constant speed of \(1 {cms}^{-1}\). At some instant, a part of \(L\) is in a uniform magnetic field of \(1 T\), perpendicular to the plane of loop. If the resistance of \(L\) is \(2.7 \,\Omega\), the current in the loop at that instant is found out to be \({N} \times 10^{-4} {~A}\)
\(\text { Find N. }\left[\text { Take } \dfrac{4}{3}=1.3\right]\)

358433 A circular loop of radius \(r\) is moved with a velocity \(v\) as shown in the diagram. The work needed to maintain its velocity constant is :

358434 A wire of length \(1\;m\) is moving at a speed of 2 \(m{s^{ - 1}}\) perpendicular to its length and a homogeneous magnetic field of \(0.5\;T\). The ends of the wire are joined to a circuit of resistance \(6 \Omega\). The rate at which work is being done to keep the wire moving at constant speed is:

358435 A square loop of area \(25\;c{m^2}\) has a resistance of \(10 \Omega\). The loop is placed in uniform magnetic field of magnitude \(40.0\,T.\) The plane of loop is perpendicular to the magnetic field. The work done in pulling the loop out of the magnetic field slowly and uniformly in \(1.0\,\sec ,\) will be

358431 A \(0.1\;m\) long conductor carrying a current of 50 \(A\) is held perpendicular to a magnetic field of \(1.25\,mT\). The mechanical power required to move the conductor with a speed of \(1\;m{s^{ - 1}}\) is

358432 The figure shows a square loop \({L}\) of side \(5 {~cm}\) which is connected to a network of resistances. The whole setup is moving towards right with a constant speed of \(1 {cms}^{-1}\). At some instant, a part of \(L\) is in a uniform magnetic field of \(1 T\), perpendicular to the plane of loop. If the resistance of \(L\) is \(2.7 \,\Omega\), the current in the loop at that instant is found out to be \({N} \times 10^{-4} {~A}\)
\(\text { Find N. }\left[\text { Take } \dfrac{4}{3}=1.3\right]\)

358433 A circular loop of radius \(r\) is moved with a velocity \(v\) as shown in the diagram. The work needed to maintain its velocity constant is :

358434 A wire of length \(1\;m\) is moving at a speed of 2 \(m{s^{ - 1}}\) perpendicular to its length and a homogeneous magnetic field of \(0.5\;T\). The ends of the wire are joined to a circuit of resistance \(6 \Omega\). The rate at which work is being done to keep the wire moving at constant speed is:

358435 A square loop of area \(25\;c{m^2}\) has a resistance of \(10 \Omega\). The loop is placed in uniform magnetic field of magnitude \(40.0\,T.\) The plane of loop is perpendicular to the magnetic field. The work done in pulling the loop out of the magnetic field slowly and uniformly in \(1.0\,\sec ,\) will be

358431 A \(0.1\;m\) long conductor carrying a current of 50 \(A\) is held perpendicular to a magnetic field of \(1.25\,mT\). The mechanical power required to move the conductor with a speed of \(1\;m{s^{ - 1}}\) is

358432 The figure shows a square loop \({L}\) of side \(5 {~cm}\) which is connected to a network of resistances. The whole setup is moving towards right with a constant speed of \(1 {cms}^{-1}\). At some instant, a part of \(L\) is in a uniform magnetic field of \(1 T\), perpendicular to the plane of loop. If the resistance of \(L\) is \(2.7 \,\Omega\), the current in the loop at that instant is found out to be \({N} \times 10^{-4} {~A}\)
\(\text { Find N. }\left[\text { Take } \dfrac{4}{3}=1.3\right]\)

358433 A circular loop of radius \(r\) is moved with a velocity \(v\) as shown in the diagram. The work needed to maintain its velocity constant is :

358434 A wire of length \(1\;m\) is moving at a speed of 2 \(m{s^{ - 1}}\) perpendicular to its length and a homogeneous magnetic field of \(0.5\;T\). The ends of the wire are joined to a circuit of resistance \(6 \Omega\). The rate at which work is being done to keep the wire moving at constant speed is:

358435 A square loop of area \(25\;c{m^2}\) has a resistance of \(10 \Omega\). The loop is placed in uniform magnetic field of magnitude \(40.0\,T.\) The plane of loop is perpendicular to the magnetic field. The work done in pulling the loop out of the magnetic field slowly and uniformly in \(1.0\,\sec ,\) will be

358431 A \(0.1\;m\) long conductor carrying a current of 50 \(A\) is held perpendicular to a magnetic field of \(1.25\,mT\). The mechanical power required to move the conductor with a speed of \(1\;m{s^{ - 1}}\) is

358432 The figure shows a square loop \({L}\) of side \(5 {~cm}\) which is connected to a network of resistances. The whole setup is moving towards right with a constant speed of \(1 {cms}^{-1}\). At some instant, a part of \(L\) is in a uniform magnetic field of \(1 T\), perpendicular to the plane of loop. If the resistance of \(L\) is \(2.7 \,\Omega\), the current in the loop at that instant is found out to be \({N} \times 10^{-4} {~A}\)
\(\text { Find N. }\left[\text { Take } \dfrac{4}{3}=1.3\right]\)

358433 A circular loop of radius \(r\) is moved with a velocity \(v\) as shown in the diagram. The work needed to maintain its velocity constant is :

358434 A wire of length \(1\;m\) is moving at a speed of 2 \(m{s^{ - 1}}\) perpendicular to its length and a homogeneous magnetic field of \(0.5\;T\). The ends of the wire are joined to a circuit of resistance \(6 \Omega\). The rate at which work is being done to keep the wire moving at constant speed is:

358435 A square loop of area \(25\;c{m^2}\) has a resistance of \(10 \Omega\). The loop is placed in uniform magnetic field of magnitude \(40.0\,T.\) The plane of loop is perpendicular to the magnetic field. The work done in pulling the loop out of the magnetic field slowly and uniformly in \(1.0\,\sec ,\) will be