320210
The Arrhenius equation for trans isomerisation of 2-butene and 1-butene nitrile are given as follows:
(i) For 2-butene; \({\rm{k}}\left( {{{\rm{s}}^{{\rm{ - 1}}}}} \right){\rm{ = 1}}{{\rm{0}}^{{\rm{13}}{\rm{.8}}}}{{\rm{e}}^{{\rm{( - 263}}{\rm{.5}}\;{\rm{kJ/mol//RT)}}}}\)
(ii) For 2-butene nitrile ; \({\text{k'}}\left( {{{\text{s}}^{{\text{ - 1}}}}} \right){\text{ = 1}}{{\text{0}}^{{\text{11}}}}{\text{ex}}{{\text{p}}^{{\text{ - 214}}{\text{.5kmo}}{{\text{\Gamma }}^{{\text{ - 1/RT}}}}}}\)
The temperature at which \({\text{k = k'}}\) is
320212 The rate of a reaction A doubles on increasing the temperature from 300 to \(310 \mathrm{~K}\). By how much, the temperature of reaction \(\mathrm{B}\) should be increased from \(300 \mathrm{~K}\) so that rate doubles if activation energy of the reaction \(B\) is twice that of reaction \(\mathrm{A}\).
320213
Consider the following reaction,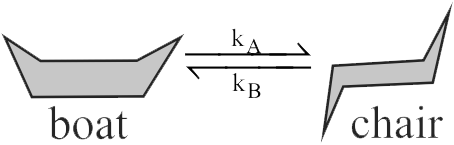
The reaction is of first order in each diagram, with an equilibrium constant of \({10^4}\). For the conversion of chair form to boat form \({{\text{e}}^{{\text{ - E/aRT}}}} = 4.35 \times {10^{ - 8}}\) at 298 K with pre-exponential factor of \({10^{12}}{\mkern 1mu} {{\text{s}}^{ - 1}}.\) Apparent rate constant \(( = {{\text{k}}_{\text{A}}}/{{\text{k}}_{\text{B}}})\) at 298 K is
320210
The Arrhenius equation for trans isomerisation of 2-butene and 1-butene nitrile are given as follows:
(i) For 2-butene; \({\rm{k}}\left( {{{\rm{s}}^{{\rm{ - 1}}}}} \right){\rm{ = 1}}{{\rm{0}}^{{\rm{13}}{\rm{.8}}}}{{\rm{e}}^{{\rm{( - 263}}{\rm{.5}}\;{\rm{kJ/mol//RT)}}}}\)
(ii) For 2-butene nitrile ; \({\text{k'}}\left( {{{\text{s}}^{{\text{ - 1}}}}} \right){\text{ = 1}}{{\text{0}}^{{\text{11}}}}{\text{ex}}{{\text{p}}^{{\text{ - 214}}{\text{.5kmo}}{{\text{\Gamma }}^{{\text{ - 1/RT}}}}}}\)
The temperature at which \({\text{k = k'}}\) is
320212 The rate of a reaction A doubles on increasing the temperature from 300 to \(310 \mathrm{~K}\). By how much, the temperature of reaction \(\mathrm{B}\) should be increased from \(300 \mathrm{~K}\) so that rate doubles if activation energy of the reaction \(B\) is twice that of reaction \(\mathrm{A}\).
320213
Consider the following reaction,
The reaction is of first order in each diagram, with an equilibrium constant of \({10^4}\). For the conversion of chair form to boat form \({{\text{e}}^{{\text{ - E/aRT}}}} = 4.35 \times {10^{ - 8}}\) at 298 K with pre-exponential factor of \({10^{12}}{\mkern 1mu} {{\text{s}}^{ - 1}}.\) Apparent rate constant \(( = {{\text{k}}_{\text{A}}}/{{\text{k}}_{\text{B}}})\) at 298 K is
320210
The Arrhenius equation for trans isomerisation of 2-butene and 1-butene nitrile are given as follows:
(i) For 2-butene; \({\rm{k}}\left( {{{\rm{s}}^{{\rm{ - 1}}}}} \right){\rm{ = 1}}{{\rm{0}}^{{\rm{13}}{\rm{.8}}}}{{\rm{e}}^{{\rm{( - 263}}{\rm{.5}}\;{\rm{kJ/mol//RT)}}}}\)
(ii) For 2-butene nitrile ; \({\text{k'}}\left( {{{\text{s}}^{{\text{ - 1}}}}} \right){\text{ = 1}}{{\text{0}}^{{\text{11}}}}{\text{ex}}{{\text{p}}^{{\text{ - 214}}{\text{.5kmo}}{{\text{\Gamma }}^{{\text{ - 1/RT}}}}}}\)
The temperature at which \({\text{k = k'}}\) is
320212 The rate of a reaction A doubles on increasing the temperature from 300 to \(310 \mathrm{~K}\). By how much, the temperature of reaction \(\mathrm{B}\) should be increased from \(300 \mathrm{~K}\) so that rate doubles if activation energy of the reaction \(B\) is twice that of reaction \(\mathrm{A}\).
320213
Consider the following reaction,
The reaction is of first order in each diagram, with an equilibrium constant of \({10^4}\). For the conversion of chair form to boat form \({{\text{e}}^{{\text{ - E/aRT}}}} = 4.35 \times {10^{ - 8}}\) at 298 K with pre-exponential factor of \({10^{12}}{\mkern 1mu} {{\text{s}}^{ - 1}}.\) Apparent rate constant \(( = {{\text{k}}_{\text{A}}}/{{\text{k}}_{\text{B}}})\) at 298 K is
320210
The Arrhenius equation for trans isomerisation of 2-butene and 1-butene nitrile are given as follows:
(i) For 2-butene; \({\rm{k}}\left( {{{\rm{s}}^{{\rm{ - 1}}}}} \right){\rm{ = 1}}{{\rm{0}}^{{\rm{13}}{\rm{.8}}}}{{\rm{e}}^{{\rm{( - 263}}{\rm{.5}}\;{\rm{kJ/mol//RT)}}}}\)
(ii) For 2-butene nitrile ; \({\text{k'}}\left( {{{\text{s}}^{{\text{ - 1}}}}} \right){\text{ = 1}}{{\text{0}}^{{\text{11}}}}{\text{ex}}{{\text{p}}^{{\text{ - 214}}{\text{.5kmo}}{{\text{\Gamma }}^{{\text{ - 1/RT}}}}}}\)
The temperature at which \({\text{k = k'}}\) is
320212 The rate of a reaction A doubles on increasing the temperature from 300 to \(310 \mathrm{~K}\). By how much, the temperature of reaction \(\mathrm{B}\) should be increased from \(300 \mathrm{~K}\) so that rate doubles if activation energy of the reaction \(B\) is twice that of reaction \(\mathrm{A}\).
320213
Consider the following reaction,
The reaction is of first order in each diagram, with an equilibrium constant of \({10^4}\). For the conversion of chair form to boat form \({{\text{e}}^{{\text{ - E/aRT}}}} = 4.35 \times {10^{ - 8}}\) at 298 K with pre-exponential factor of \({10^{12}}{\mkern 1mu} {{\text{s}}^{ - 1}}.\) Apparent rate constant \(( = {{\text{k}}_{\text{A}}}/{{\text{k}}_{\text{B}}})\) at 298 K is
320210
The Arrhenius equation for trans isomerisation of 2-butene and 1-butene nitrile are given as follows:
(i) For 2-butene; \({\rm{k}}\left( {{{\rm{s}}^{{\rm{ - 1}}}}} \right){\rm{ = 1}}{{\rm{0}}^{{\rm{13}}{\rm{.8}}}}{{\rm{e}}^{{\rm{( - 263}}{\rm{.5}}\;{\rm{kJ/mol//RT)}}}}\)
(ii) For 2-butene nitrile ; \({\text{k'}}\left( {{{\text{s}}^{{\text{ - 1}}}}} \right){\text{ = 1}}{{\text{0}}^{{\text{11}}}}{\text{ex}}{{\text{p}}^{{\text{ - 214}}{\text{.5kmo}}{{\text{\Gamma }}^{{\text{ - 1/RT}}}}}}\)
The temperature at which \({\text{k = k'}}\) is
320212 The rate of a reaction A doubles on increasing the temperature from 300 to \(310 \mathrm{~K}\). By how much, the temperature of reaction \(\mathrm{B}\) should be increased from \(300 \mathrm{~K}\) so that rate doubles if activation energy of the reaction \(B\) is twice that of reaction \(\mathrm{A}\).
320213
Consider the following reaction,
The reaction is of first order in each diagram, with an equilibrium constant of \({10^4}\). For the conversion of chair form to boat form \({{\text{e}}^{{\text{ - E/aRT}}}} = 4.35 \times {10^{ - 8}}\) at 298 K with pre-exponential factor of \({10^{12}}{\mkern 1mu} {{\text{s}}^{ - 1}}.\) Apparent rate constant \(( = {{\text{k}}_{\text{A}}}/{{\text{k}}_{\text{B}}})\) at 298 K is