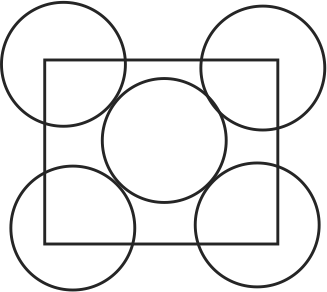
318681 Metal M of radius 50 nm is crystallized in fcc type and made cubical crystal such that face of unit cells aligned with face of cubical crystal. If the total number of metal atoms of \({\mathrm{M}}\) at all faces of cubical crystal is \({\mathrm{6 \times 10^{30}}}\), then the area of one face of cubical crystal is
318682 A bcc lattice is made up of hollow spheres of \({\mathrm{B}}\). Spheres of solids \({\mathrm{A}}\) are present in hollow spheres of \({\mathrm{B}}\). The radius of \({\mathrm{A}}\) is half of the radius of \({\mathrm{B}}\). The ratio of total volume of spheres of \({\mathrm{B}}\) unoccupied by \({\mathrm{A}}\) in a unit cell and volume of unit cell is \({\mathrm{A \times \dfrac{\pi \sqrt{3}}{64}}}\). Find the value of \({\mathrm{A}}\).
318681 Metal M of radius 50 nm is crystallized in fcc type and made cubical crystal such that face of unit cells aligned with face of cubical crystal. If the total number of metal atoms of \({\mathrm{M}}\) at all faces of cubical crystal is \({\mathrm{6 \times 10^{30}}}\), then the area of one face of cubical crystal is
318682 A bcc lattice is made up of hollow spheres of \({\mathrm{B}}\). Spheres of solids \({\mathrm{A}}\) are present in hollow spheres of \({\mathrm{B}}\). The radius of \({\mathrm{A}}\) is half of the radius of \({\mathrm{B}}\). The ratio of total volume of spheres of \({\mathrm{B}}\) unoccupied by \({\mathrm{A}}\) in a unit cell and volume of unit cell is \({\mathrm{A \times \dfrac{\pi \sqrt{3}}{64}}}\). Find the value of \({\mathrm{A}}\).
318681 Metal M of radius 50 nm is crystallized in fcc type and made cubical crystal such that face of unit cells aligned with face of cubical crystal. If the total number of metal atoms of \({\mathrm{M}}\) at all faces of cubical crystal is \({\mathrm{6 \times 10^{30}}}\), then the area of one face of cubical crystal is
318682 A bcc lattice is made up of hollow spheres of \({\mathrm{B}}\). Spheres of solids \({\mathrm{A}}\) are present in hollow spheres of \({\mathrm{B}}\). The radius of \({\mathrm{A}}\) is half of the radius of \({\mathrm{B}}\). The ratio of total volume of spheres of \({\mathrm{B}}\) unoccupied by \({\mathrm{A}}\) in a unit cell and volume of unit cell is \({\mathrm{A \times \dfrac{\pi \sqrt{3}}{64}}}\). Find the value of \({\mathrm{A}}\).
318681 Metal M of radius 50 nm is crystallized in fcc type and made cubical crystal such that face of unit cells aligned with face of cubical crystal. If the total number of metal atoms of \({\mathrm{M}}\) at all faces of cubical crystal is \({\mathrm{6 \times 10^{30}}}\), then the area of one face of cubical crystal is
318682 A bcc lattice is made up of hollow spheres of \({\mathrm{B}}\). Spheres of solids \({\mathrm{A}}\) are present in hollow spheres of \({\mathrm{B}}\). The radius of \({\mathrm{A}}\) is half of the radius of \({\mathrm{B}}\). The ratio of total volume of spheres of \({\mathrm{B}}\) unoccupied by \({\mathrm{A}}\) in a unit cell and volume of unit cell is \({\mathrm{A \times \dfrac{\pi \sqrt{3}}{64}}}\). Find the value of \({\mathrm{A}}\).
318681 Metal M of radius 50 nm is crystallized in fcc type and made cubical crystal such that face of unit cells aligned with face of cubical crystal. If the total number of metal atoms of \({\mathrm{M}}\) at all faces of cubical crystal is \({\mathrm{6 \times 10^{30}}}\), then the area of one face of cubical crystal is
318682 A bcc lattice is made up of hollow spheres of \({\mathrm{B}}\). Spheres of solids \({\mathrm{A}}\) are present in hollow spheres of \({\mathrm{B}}\). The radius of \({\mathrm{A}}\) is half of the radius of \({\mathrm{B}}\). The ratio of total volume of spheres of \({\mathrm{B}}\) unoccupied by \({\mathrm{A}}\) in a unit cell and volume of unit cell is \({\mathrm{A \times \dfrac{\pi \sqrt{3}}{64}}}\). Find the value of \({\mathrm{A}}\).