358308 A cubical Gaussian surface has side of length \(a = 10\;cm\). Electric field lines are parallel to \(x - \)axis as shown. The magnitudes of electric fields through surfaces \(A B C D\) and \(E F G H\) are \(6 k N C^{-1}\) and \(9 k N C^{-1}\) respectively. Then the total charge enclosed by the cube is \(\left[ {{\rm{Take}}\,\,{\varepsilon _0} = 9 \times {{10}^{ - 12}}F{m^{ - 1}}} \right]\)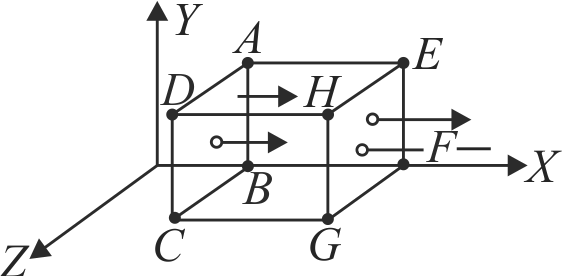

358309 The inward and outward electric flux for a closed surface in units of \(N - {m^2}{\text{/}}C\) are respectively \(8 \times {10^3}\) and \(4 \times {10^3}\) . Then the total charge inside the surface is [where \({\varepsilon _0} = \) permittivity constant]

358310 If there is only one type of charge in the universe, then (\(\overrightarrow E = \) Electric field, \(d\overrightarrow S = \) Area vector)

358311 Electric flux emanating through a surface element \(d\vec S = 5\,\hat i\) placed in an electric field \(\vec E = 4\hat i + 4\hat j + 4\hat k\) is

358308 A cubical Gaussian surface has side of length \(a = 10\;cm\). Electric field lines are parallel to \(x - \)axis as shown. The magnitudes of electric fields through surfaces \(A B C D\) and \(E F G H\) are \(6 k N C^{-1}\) and \(9 k N C^{-1}\) respectively. Then the total charge enclosed by the cube is \(\left[ {{\rm{Take}}\,\,{\varepsilon _0} = 9 \times {{10}^{ - 12}}F{m^{ - 1}}} \right]\)

358309 The inward and outward electric flux for a closed surface in units of \(N - {m^2}{\text{/}}C\) are respectively \(8 \times {10^3}\) and \(4 \times {10^3}\) . Then the total charge inside the surface is [where \({\varepsilon _0} = \) permittivity constant]

358310 If there is only one type of charge in the universe, then (\(\overrightarrow E = \) Electric field, \(d\overrightarrow S = \) Area vector)

358311 Electric flux emanating through a surface element \(d\vec S = 5\,\hat i\) placed in an electric field \(\vec E = 4\hat i + 4\hat j + 4\hat k\) is

358308 A cubical Gaussian surface has side of length \(a = 10\;cm\). Electric field lines are parallel to \(x - \)axis as shown. The magnitudes of electric fields through surfaces \(A B C D\) and \(E F G H\) are \(6 k N C^{-1}\) and \(9 k N C^{-1}\) respectively. Then the total charge enclosed by the cube is \(\left[ {{\rm{Take}}\,\,{\varepsilon _0} = 9 \times {{10}^{ - 12}}F{m^{ - 1}}} \right]\)

358309 The inward and outward electric flux for a closed surface in units of \(N - {m^2}{\text{/}}C\) are respectively \(8 \times {10^3}\) and \(4 \times {10^3}\) . Then the total charge inside the surface is [where \({\varepsilon _0} = \) permittivity constant]

358310 If there is only one type of charge in the universe, then (\(\overrightarrow E = \) Electric field, \(d\overrightarrow S = \) Area vector)

358311 Electric flux emanating through a surface element \(d\vec S = 5\,\hat i\) placed in an electric field \(\vec E = 4\hat i + 4\hat j + 4\hat k\) is

358308 A cubical Gaussian surface has side of length \(a = 10\;cm\). Electric field lines are parallel to \(x - \)axis as shown. The magnitudes of electric fields through surfaces \(A B C D\) and \(E F G H\) are \(6 k N C^{-1}\) and \(9 k N C^{-1}\) respectively. Then the total charge enclosed by the cube is \(\left[ {{\rm{Take}}\,\,{\varepsilon _0} = 9 \times {{10}^{ - 12}}F{m^{ - 1}}} \right]\)

358309 The inward and outward electric flux for a closed surface in units of \(N - {m^2}{\text{/}}C\) are respectively \(8 \times {10^3}\) and \(4 \times {10^3}\) . Then the total charge inside the surface is [where \({\varepsilon _0} = \) permittivity constant]

358310 If there is only one type of charge in the universe, then (\(\overrightarrow E = \) Electric field, \(d\overrightarrow S = \) Area vector)

358311 Electric flux emanating through a surface element \(d\vec S = 5\,\hat i\) placed in an electric field \(\vec E = 4\hat i + 4\hat j + 4\hat k\) is