357949
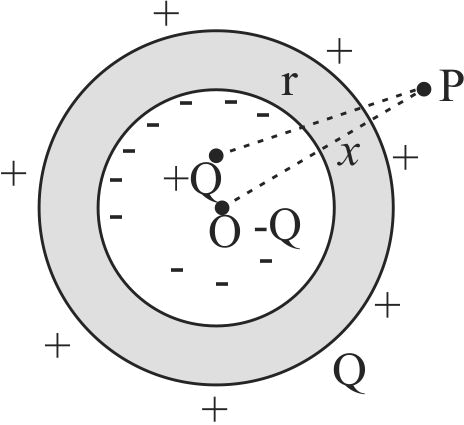
The adjacent diagram shows a charge +\(Q\) held on an insulating support \(S\) and enclosed by a hollow spherical conductor. \(O\) represents the centre of the spherical conductor and \(P\) is a point such that \(OP = x\,{\rm{and}}\,SP = r\). The electric field at a point \(P\) will be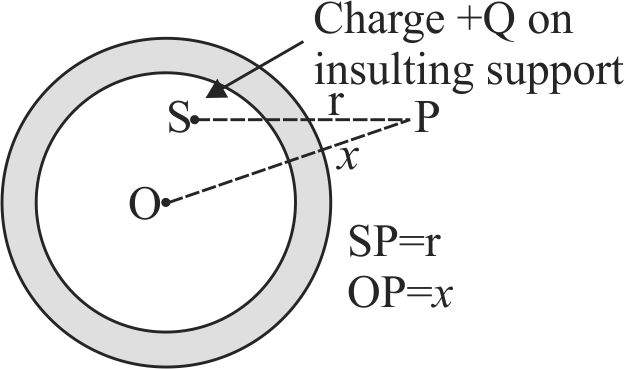
357951
An early model for an atom considered it to have a positively charged point nucleus of charge \(Ze\), surrounded by a uniform density of negative charge upto a radius \(R\). The atom as a whole is neutral. The electric field at a distance \(r\) from the nucleus is \((r < R)\)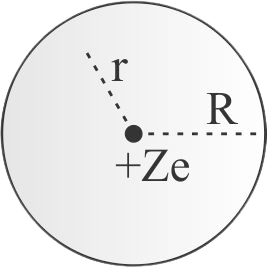
357952
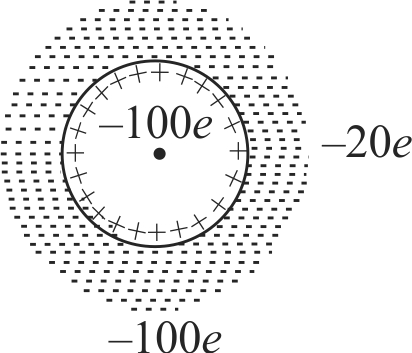
\({S_{1}}\) and \({S_{2}}\) are two hollow concentric spheres with charge \({q}\) and \({2 q}\). Space between \({S_{1}}\) and \({S_{2}}\) is filled with a dielectric of dielectric constants.
The ratio of flux through \({S_{2}}\) and flux through \({S_{1}}\) is \({K}\). Then, find the value of \({\dfrac{9 K}{11}}\)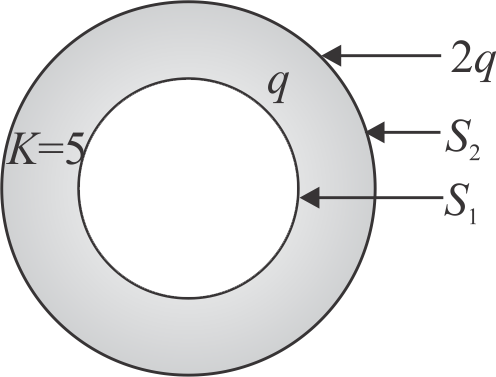
357953 A sphere \(S_{1}\) of radius \(R\), encloses a total charge \(q\). If there is another concentric sphere \(S_{2}\) of radius \(2 R\) and there be no additional charges between \(S_{1}\) and \(S_{2}\). What is the ratio of electric flux through \(S_{1}\) and \(S_{2}\) ?
357949
The adjacent diagram shows a charge +\(Q\) held on an insulating support \(S\) and enclosed by a hollow spherical conductor. \(O\) represents the centre of the spherical conductor and \(P\) is a point such that \(OP = x\,{\rm{and}}\,SP = r\). The electric field at a point \(P\) will be
357951
An early model for an atom considered it to have a positively charged point nucleus of charge \(Ze\), surrounded by a uniform density of negative charge upto a radius \(R\). The atom as a whole is neutral. The electric field at a distance \(r\) from the nucleus is \((r < R)\)
357952
\({S_{1}}\) and \({S_{2}}\) are two hollow concentric spheres with charge \({q}\) and \({2 q}\). Space between \({S_{1}}\) and \({S_{2}}\) is filled with a dielectric of dielectric constants.
The ratio of flux through \({S_{2}}\) and flux through \({S_{1}}\) is \({K}\). Then, find the value of \({\dfrac{9 K}{11}}\)
357953 A sphere \(S_{1}\) of radius \(R\), encloses a total charge \(q\). If there is another concentric sphere \(S_{2}\) of radius \(2 R\) and there be no additional charges between \(S_{1}\) and \(S_{2}\). What is the ratio of electric flux through \(S_{1}\) and \(S_{2}\) ?
357949
The adjacent diagram shows a charge +\(Q\) held on an insulating support \(S\) and enclosed by a hollow spherical conductor. \(O\) represents the centre of the spherical conductor and \(P\) is a point such that \(OP = x\,{\rm{and}}\,SP = r\). The electric field at a point \(P\) will be
357951
An early model for an atom considered it to have a positively charged point nucleus of charge \(Ze\), surrounded by a uniform density of negative charge upto a radius \(R\). The atom as a whole is neutral. The electric field at a distance \(r\) from the nucleus is \((r < R)\)
357952
\({S_{1}}\) and \({S_{2}}\) are two hollow concentric spheres with charge \({q}\) and \({2 q}\). Space between \({S_{1}}\) and \({S_{2}}\) is filled with a dielectric of dielectric constants.
The ratio of flux through \({S_{2}}\) and flux through \({S_{1}}\) is \({K}\). Then, find the value of \({\dfrac{9 K}{11}}\)
357953 A sphere \(S_{1}\) of radius \(R\), encloses a total charge \(q\). If there is another concentric sphere \(S_{2}\) of radius \(2 R\) and there be no additional charges between \(S_{1}\) and \(S_{2}\). What is the ratio of electric flux through \(S_{1}\) and \(S_{2}\) ?
357949
The adjacent diagram shows a charge +\(Q\) held on an insulating support \(S\) and enclosed by a hollow spherical conductor. \(O\) represents the centre of the spherical conductor and \(P\) is a point such that \(OP = x\,{\rm{and}}\,SP = r\). The electric field at a point \(P\) will be
357951
An early model for an atom considered it to have a positively charged point nucleus of charge \(Ze\), surrounded by a uniform density of negative charge upto a radius \(R\). The atom as a whole is neutral. The electric field at a distance \(r\) from the nucleus is \((r < R)\)
357952
\({S_{1}}\) and \({S_{2}}\) are two hollow concentric spheres with charge \({q}\) and \({2 q}\). Space between \({S_{1}}\) and \({S_{2}}\) is filled with a dielectric of dielectric constants.
The ratio of flux through \({S_{2}}\) and flux through \({S_{1}}\) is \({K}\). Then, find the value of \({\dfrac{9 K}{11}}\)
357953 A sphere \(S_{1}\) of radius \(R\), encloses a total charge \(q\). If there is another concentric sphere \(S_{2}\) of radius \(2 R\) and there be no additional charges between \(S_{1}\) and \(S_{2}\). What is the ratio of electric flux through \(S_{1}\) and \(S_{2}\) ?
357949
The adjacent diagram shows a charge +\(Q\) held on an insulating support \(S\) and enclosed by a hollow spherical conductor. \(O\) represents the centre of the spherical conductor and \(P\) is a point such that \(OP = x\,{\rm{and}}\,SP = r\). The electric field at a point \(P\) will be
357951
An early model for an atom considered it to have a positively charged point nucleus of charge \(Ze\), surrounded by a uniform density of negative charge upto a radius \(R\). The atom as a whole is neutral. The electric field at a distance \(r\) from the nucleus is \((r < R)\)
357952
\({S_{1}}\) and \({S_{2}}\) are two hollow concentric spheres with charge \({q}\) and \({2 q}\). Space between \({S_{1}}\) and \({S_{2}}\) is filled with a dielectric of dielectric constants.
The ratio of flux through \({S_{2}}\) and flux through \({S_{1}}\) is \({K}\). Then, find the value of \({\dfrac{9 K}{11}}\)
357953 A sphere \(S_{1}\) of radius \(R\), encloses a total charge \(q\). If there is another concentric sphere \(S_{2}\) of radius \(2 R\) and there be no additional charges between \(S_{1}\) and \(S_{2}\). What is the ratio of electric flux through \(S_{1}\) and \(S_{2}\) ?