357036
Two cylindrical rods of uniform cross-section area \({A}\) and \({2 A}\), having free electrons per unit volume \({2 n}\) and \({n}\), respectively, are joined in series. A current \({I}\) flows through them in steady state. The ratio of drift velocity of free electron in left rod to drift velocity of electron in the right \({\operatorname{rod},\left(\dfrac{v_{L}}{v_{R}}\right)}\), is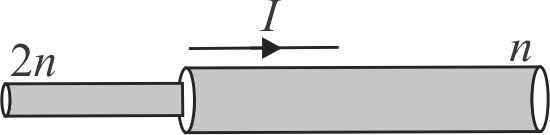
357037 The drift velocity of electrons for a conductor connected in an electrical circuit is \(V_{d}\). The conductor is now replaced by another conductor with same material and same length but double the area of cross section. The applied voltage remains same. The new drift velocity of electrons will be
357036
Two cylindrical rods of uniform cross-section area \({A}\) and \({2 A}\), having free electrons per unit volume \({2 n}\) and \({n}\), respectively, are joined in series. A current \({I}\) flows through them in steady state. The ratio of drift velocity of free electron in left rod to drift velocity of electron in the right \({\operatorname{rod},\left(\dfrac{v_{L}}{v_{R}}\right)}\), is
357037 The drift velocity of electrons for a conductor connected in an electrical circuit is \(V_{d}\). The conductor is now replaced by another conductor with same material and same length but double the area of cross section. The applied voltage remains same. The new drift velocity of electrons will be
357036
Two cylindrical rods of uniform cross-section area \({A}\) and \({2 A}\), having free electrons per unit volume \({2 n}\) and \({n}\), respectively, are joined in series. A current \({I}\) flows through them in steady state. The ratio of drift velocity of free electron in left rod to drift velocity of electron in the right \({\operatorname{rod},\left(\dfrac{v_{L}}{v_{R}}\right)}\), is
357037 The drift velocity of electrons for a conductor connected in an electrical circuit is \(V_{d}\). The conductor is now replaced by another conductor with same material and same length but double the area of cross section. The applied voltage remains same. The new drift velocity of electrons will be
357036
Two cylindrical rods of uniform cross-section area \({A}\) and \({2 A}\), having free electrons per unit volume \({2 n}\) and \({n}\), respectively, are joined in series. A current \({I}\) flows through them in steady state. The ratio of drift velocity of free electron in left rod to drift velocity of electron in the right \({\operatorname{rod},\left(\dfrac{v_{L}}{v_{R}}\right)}\), is
357037 The drift velocity of electrons for a conductor connected in an electrical circuit is \(V_{d}\). The conductor is now replaced by another conductor with same material and same length but double the area of cross section. The applied voltage remains same. The new drift velocity of electrons will be