356893
A battery of \(\varepsilon \) and internal resistance r is connected across a resistance \(R\). Resistance \(R\) can be adjusted to any value greater than are equal to zero. A graph is plotted between the current (\(I\)) passing through the resistance and potential difference (\(V\)) across it.
Select the correct alternative (\(s\)):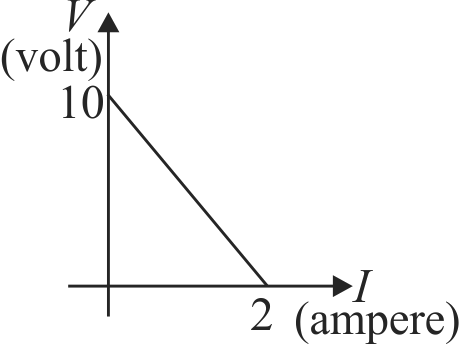
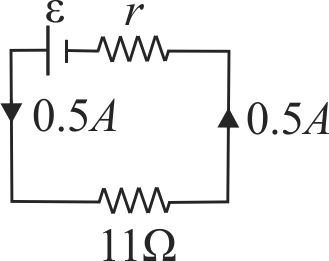
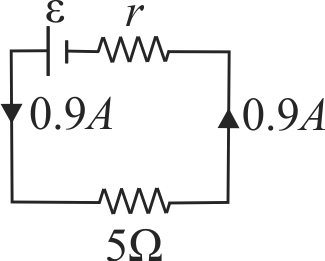
356894 When a resistor of \(11\,\Omega\) is connected in series with an electric cell, the current flowing in it is \(0.5\;A\). Instead when a resistor of \(5\, \Omega\) is connected to the same electric cell in series, the current increases by \(0.4\;A\). The internal resistance of the cell is
356893
A battery of \(\varepsilon \) and internal resistance r is connected across a resistance \(R\). Resistance \(R\) can be adjusted to any value greater than are equal to zero. A graph is plotted between the current (\(I\)) passing through the resistance and potential difference (\(V\)) across it.
Select the correct alternative (\(s\)):
356894 When a resistor of \(11\,\Omega\) is connected in series with an electric cell, the current flowing in it is \(0.5\;A\). Instead when a resistor of \(5\, \Omega\) is connected to the same electric cell in series, the current increases by \(0.4\;A\). The internal resistance of the cell is
356893
A battery of \(\varepsilon \) and internal resistance r is connected across a resistance \(R\). Resistance \(R\) can be adjusted to any value greater than are equal to zero. A graph is plotted between the current (\(I\)) passing through the resistance and potential difference (\(V\)) across it.
Select the correct alternative (\(s\)):
356894 When a resistor of \(11\,\Omega\) is connected in series with an electric cell, the current flowing in it is \(0.5\;A\). Instead when a resistor of \(5\, \Omega\) is connected to the same electric cell in series, the current increases by \(0.4\;A\). The internal resistance of the cell is
356893
A battery of \(\varepsilon \) and internal resistance r is connected across a resistance \(R\). Resistance \(R\) can be adjusted to any value greater than are equal to zero. A graph is plotted between the current (\(I\)) passing through the resistance and potential difference (\(V\)) across it.
Select the correct alternative (\(s\)):
356894 When a resistor of \(11\,\Omega\) is connected in series with an electric cell, the current flowing in it is \(0.5\;A\). Instead when a resistor of \(5\, \Omega\) is connected to the same electric cell in series, the current increases by \(0.4\;A\). The internal resistance of the cell is
356893
A battery of \(\varepsilon \) and internal resistance r is connected across a resistance \(R\). Resistance \(R\) can be adjusted to any value greater than are equal to zero. A graph is plotted between the current (\(I\)) passing through the resistance and potential difference (\(V\)) across it.
Select the correct alternative (\(s\)):
356894 When a resistor of \(11\,\Omega\) is connected in series with an electric cell, the current flowing in it is \(0.5\;A\). Instead when a resistor of \(5\, \Omega\) is connected to the same electric cell in series, the current increases by \(0.4\;A\). The internal resistance of the cell is