356158
In an \(LCR\) series circuit connected to an \(ac\) source, the supply voltage is
\(V = {V_0}\sin \left( {100\pi t + \frac{\pi }{6}} \right) \cdot {V_L} = 40V,\)
\({V_R} = 40V,\;Z = 5\Omega \;{\mathop{\rm and}\nolimits} R = 4\Omega \) Then match the column I and II.
| Column I | Column II |
|---|---|
| A. Peak current (in A) | P. \(10\sqrt 2 \) |
| B. \({V_0}\) (in volts) | Q. \(50\sqrt 2 \) |
| C. \({X_L}({\mathop{\rm in}\nolimits} \,\Omega )\) | R. \(4\) |
| D. \({X_C}({\mathop{\rm in}\nolimits} \,\Omega )\) | S. \(1\) |
356158
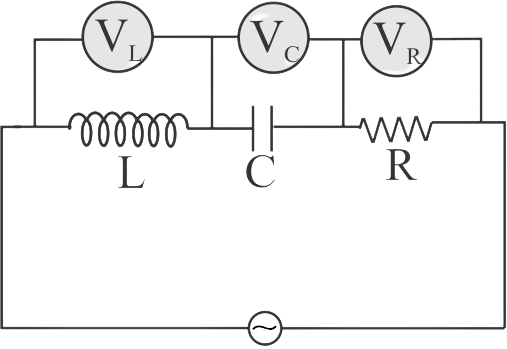
In an \(LCR\) series circuit connected to an \(ac\) source, the supply voltage is
\(V = {V_0}\sin \left( {100\pi t + \frac{\pi }{6}} \right) \cdot {V_L} = 40V,\)
\({V_R} = 40V,\;Z = 5\Omega \;{\mathop{\rm and}\nolimits} R = 4\Omega \) Then match the column I and II.
| Column I | Column II |
|---|---|
| A. Peak current (in A) | P. \(10\sqrt 2 \) |
| B. \({V_0}\) (in volts) | Q. \(50\sqrt 2 \) |
| C. \({X_L}({\mathop{\rm in}\nolimits} \,\Omega )\) | R. \(4\) |
| D. \({X_C}({\mathop{\rm in}\nolimits} \,\Omega )\) | S. \(1\) |

356158
In an \(LCR\) series circuit connected to an \(ac\) source, the supply voltage is
\(V = {V_0}\sin \left( {100\pi t + \frac{\pi }{6}} \right) \cdot {V_L} = 40V,\)
\({V_R} = 40V,\;Z = 5\Omega \;{\mathop{\rm and}\nolimits} R = 4\Omega \) Then match the column I and II.
| Column I | Column II |
|---|---|
| A. Peak current (in A) | P. \(10\sqrt 2 \) |
| B. \({V_0}\) (in volts) | Q. \(50\sqrt 2 \) |
| C. \({X_L}({\mathop{\rm in}\nolimits} \,\Omega )\) | R. \(4\) |
| D. \({X_C}({\mathop{\rm in}\nolimits} \,\Omega )\) | S. \(1\) |

356158
In an \(LCR\) series circuit connected to an \(ac\) source, the supply voltage is
\(V = {V_0}\sin \left( {100\pi t + \frac{\pi }{6}} \right) \cdot {V_L} = 40V,\)
\({V_R} = 40V,\;Z = 5\Omega \;{\mathop{\rm and}\nolimits} R = 4\Omega \) Then match the column I and II.
| Column I | Column II |
|---|---|
| A. Peak current (in A) | P. \(10\sqrt 2 \) |
| B. \({V_0}\) (in volts) | Q. \(50\sqrt 2 \) |
| C. \({X_L}({\mathop{\rm in}\nolimits} \,\Omega )\) | R. \(4\) |
| D. \({X_C}({\mathop{\rm in}\nolimits} \,\Omega )\) | S. \(1\) |
