283283 In Young's double slits experiment, the position of \(5^{\text {th }}\) bright fringe from the central maximum is \(5 \mathrm{~cm}\). The distance between slits and screen is \(1 \mathrm{~m}\) and wavelength of used monochromatic light is \(600 \mathrm{~nm}\). The separation between the slits is :
283284
In a young's double slit experiment, two slits are illuminated with a light of wavelength 800 \(\mathrm{nm}\). The line joining \(A, P\) is perpendicular to \(A_1\) \(A_2\) as shown in the figure. If the first minimum is detected at \(P\), the value of slits separation ' \(a\) ' will be.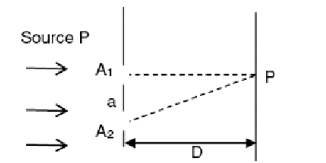
The distance of screen from slits \(D=5 \mathrm{~cm}\)
283283 In Young's double slits experiment, the position of \(5^{\text {th }}\) bright fringe from the central maximum is \(5 \mathrm{~cm}\). The distance between slits and screen is \(1 \mathrm{~m}\) and wavelength of used monochromatic light is \(600 \mathrm{~nm}\). The separation between the slits is :
283284
In a young's double slit experiment, two slits are illuminated with a light of wavelength 800 \(\mathrm{nm}\). The line joining \(A, P\) is perpendicular to \(A_1\) \(A_2\) as shown in the figure. If the first minimum is detected at \(P\), the value of slits separation ' \(a\) ' will be.
The distance of screen from slits \(D=5 \mathrm{~cm}\)
283283 In Young's double slits experiment, the position of \(5^{\text {th }}\) bright fringe from the central maximum is \(5 \mathrm{~cm}\). The distance between slits and screen is \(1 \mathrm{~m}\) and wavelength of used monochromatic light is \(600 \mathrm{~nm}\). The separation between the slits is :
283284
In a young's double slit experiment, two slits are illuminated with a light of wavelength 800 \(\mathrm{nm}\). The line joining \(A, P\) is perpendicular to \(A_1\) \(A_2\) as shown in the figure. If the first minimum is detected at \(P\), the value of slits separation ' \(a\) ' will be.
The distance of screen from slits \(D=5 \mathrm{~cm}\)
283283 In Young's double slits experiment, the position of \(5^{\text {th }}\) bright fringe from the central maximum is \(5 \mathrm{~cm}\). The distance between slits and screen is \(1 \mathrm{~m}\) and wavelength of used monochromatic light is \(600 \mathrm{~nm}\). The separation between the slits is :
283284
In a young's double slit experiment, two slits are illuminated with a light of wavelength 800 \(\mathrm{nm}\). The line joining \(A, P\) is perpendicular to \(A_1\) \(A_2\) as shown in the figure. If the first minimum is detected at \(P\), the value of slits separation ' \(a\) ' will be.
The distance of screen from slits \(D=5 \mathrm{~cm}\)
283283 In Young's double slits experiment, the position of \(5^{\text {th }}\) bright fringe from the central maximum is \(5 \mathrm{~cm}\). The distance between slits and screen is \(1 \mathrm{~m}\) and wavelength of used monochromatic light is \(600 \mathrm{~nm}\). The separation between the slits is :
283284
In a young's double slit experiment, two slits are illuminated with a light of wavelength 800 \(\mathrm{nm}\). The line joining \(A, P\) is perpendicular to \(A_1\) \(A_2\) as shown in the figure. If the first minimum is detected at \(P\), the value of slits separation ' \(a\) ' will be.
The distance of screen from slits \(D=5 \mathrm{~cm}\)
