282092
An optician prescribes a corrective lens of power $+2 \mathrm{D}$, then the focal length of the required convex lens is-
1 $10 \mathrm{~cm}$
2 $50 \mathrm{~cm}$
3 $10 \mathrm{~m}$
4 $50 \mathrm{~m}$
Explanation:
B: Given that, Power of lens $(\mathrm{P})=+2 \mathrm{D}$
Focal length $(f)=\frac{100}{P}$
$\begin{aligned}
f=\frac{100}{2} \\
f=50 \mathrm{~cm}
\end{aligned}$
AP EAMCET-07.07.2022
Ray Optics
282093
A ray of light is incident at $30^{\circ}$ from a medium of refractive index 2 into a medium of refractive index 1 . Then the angle of refraction is
1 $30^{\circ}$
2 $60^0$
3 $45^{\circ}$
4 $90^{\circ}$
Explanation:
D: Given that,
Angle of Incidence $i=30^{\circ}, \mu_1=2, \mu_2=1$
We know that,
$\begin{aligned}
\mu_1 \sin i=\mu_2 \sin r \\
2 \times \sin 30^{\circ}=1 \times \sin r \\
\sin r=\frac{2}{2}=1 \\
\quad r=\sin ^{-1}(1)=90^{\circ}
\end{aligned}$
AP EAMCET-05.07.2022
Ray Optics
282094
A beam of light both reflects and refracts at the surface between air and glass. The index of refraction of the glass is $\mathbf{1 . 4}$. If the refracted and the reflected rays are perpendicular to each other. Then the angle of incidence in the air is.
1 $\tan ^{-1}(1.4)$
2 $\sin ^{-1}\left(\frac{1}{1.4}\right)$
3 $\tan ^{-1}\left(\frac{1}{1.4}\right)$
4 $\sin ^{-1}\left(\frac{1.4}{\pi}\right)$
Explanation:
A: Given that,
Refractive index of glass $\mu_{\mathrm{g}}=1.4$
$\begin{array}{ll}
180^{\circ}=\mathrm{i}+\mathrm{r}+90^{\circ} \\
\therefore \quad & (\mathrm{i}+\mathrm{r})=90^{\circ}
\end{array}$
We know that,
$\begin{aligned}
\mu_a \sin i=\mu_g \sin r \\
1 \times \sin i=1.4 \times \sin (90-i) \\
\frac{\sin i}{\cos i}=1.4 \\
\tan i=1.4 \\
\quad i=\tan ^{-1}(1.4)
\end{aligned}$
AP EAMCET-05.07.2022
Ray Optics
282095
The distance travelled by a light ray in $1 \mathrm{~ns}$ in a glass of refractive index $\mu=1.5$ is
1 $45 \mathrm{~cm}$
2 $40 \mathrm{~cm}$
3 $30 \mathrm{~cm}$
4 $20 \mathrm{~cm}$
Explanation:
D: Given that,
Time $(\mathrm{t})=1 \mathrm{~ns}=10^{-9} \mathrm{~s}$
Refractive index $(\mu)=1.5$
Distance $(d)=$ velocity $\times$ time
$\begin{aligned}
\mathrm{d}=\frac{\mathrm{c}}{\mu} \times \mathrm{t} \\
\mathrm{d}=\frac{3 \times 10^8}{1.5} \times 1 \times 10^{-9} \\
\mathrm{~d}=0.2 \mathrm{~m}=20 \mathrm{~cm}
\end{aligned}$
Tripura-27.04.2022
Ray Optics
282096
Light enters from air into a given medium at an angle of $45^{\circ}$ with interface of the airmedium surface. After refraction, the light ray is deviated through an angle of $15^{\circ}$ from its original direction. The refractive index of the medium is:
1 1.732
2 1.333
3 1.414
4 2.732
Explanation:
C: Given, incidence angle (i) $=45^{\circ}$, deviation $(\delta)$ $=15^{\circ}$
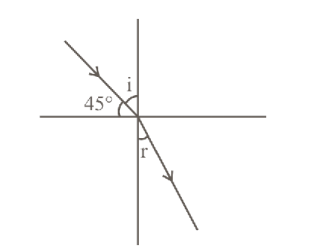
We know that,
$\begin{aligned}
\delta=i-r \\
r=45^{\circ}-15^{\circ} \\
r=30^{\circ}
\end{aligned}$
From Snell's law, refractive index of medium
$\begin{aligned}
\mu=\frac{\sin i}{\sin r} \\
\mu=\frac{\sin 45^{\circ}}{\sin 30^{\circ}} \\
\mu=\frac{1}{\sqrt{2}} \times \frac{2}{1} \\
\mu=\sqrt{2}=1.414
\end{aligned}$
282092
An optician prescribes a corrective lens of power $+2 \mathrm{D}$, then the focal length of the required convex lens is-
1 $10 \mathrm{~cm}$
2 $50 \mathrm{~cm}$
3 $10 \mathrm{~m}$
4 $50 \mathrm{~m}$
Explanation:
B: Given that, Power of lens $(\mathrm{P})=+2 \mathrm{D}$
Focal length $(f)=\frac{100}{P}$
$\begin{aligned}
f=\frac{100}{2} \\
f=50 \mathrm{~cm}
\end{aligned}$
AP EAMCET-07.07.2022
Ray Optics
282093
A ray of light is incident at $30^{\circ}$ from a medium of refractive index 2 into a medium of refractive index 1 . Then the angle of refraction is
1 $30^{\circ}$
2 $60^0$
3 $45^{\circ}$
4 $90^{\circ}$
Explanation:
D: Given that,
Angle of Incidence $i=30^{\circ}, \mu_1=2, \mu_2=1$
We know that,
$\begin{aligned}
\mu_1 \sin i=\mu_2 \sin r \\
2 \times \sin 30^{\circ}=1 \times \sin r \\
\sin r=\frac{2}{2}=1 \\
\quad r=\sin ^{-1}(1)=90^{\circ}
\end{aligned}$
AP EAMCET-05.07.2022
Ray Optics
282094
A beam of light both reflects and refracts at the surface between air and glass. The index of refraction of the glass is $\mathbf{1 . 4}$. If the refracted and the reflected rays are perpendicular to each other. Then the angle of incidence in the air is.
1 $\tan ^{-1}(1.4)$
2 $\sin ^{-1}\left(\frac{1}{1.4}\right)$
3 $\tan ^{-1}\left(\frac{1}{1.4}\right)$
4 $\sin ^{-1}\left(\frac{1.4}{\pi}\right)$
Explanation:
A: Given that,
Refractive index of glass $\mu_{\mathrm{g}}=1.4$
$\begin{array}{ll}
180^{\circ}=\mathrm{i}+\mathrm{r}+90^{\circ} \\
\therefore \quad & (\mathrm{i}+\mathrm{r})=90^{\circ}
\end{array}$
We know that,
$\begin{aligned}
\mu_a \sin i=\mu_g \sin r \\
1 \times \sin i=1.4 \times \sin (90-i) \\
\frac{\sin i}{\cos i}=1.4 \\
\tan i=1.4 \\
\quad i=\tan ^{-1}(1.4)
\end{aligned}$
AP EAMCET-05.07.2022
Ray Optics
282095
The distance travelled by a light ray in $1 \mathrm{~ns}$ in a glass of refractive index $\mu=1.5$ is
1 $45 \mathrm{~cm}$
2 $40 \mathrm{~cm}$
3 $30 \mathrm{~cm}$
4 $20 \mathrm{~cm}$
Explanation:
D: Given that,
Time $(\mathrm{t})=1 \mathrm{~ns}=10^{-9} \mathrm{~s}$
Refractive index $(\mu)=1.5$
Distance $(d)=$ velocity $\times$ time
$\begin{aligned}
\mathrm{d}=\frac{\mathrm{c}}{\mu} \times \mathrm{t} \\
\mathrm{d}=\frac{3 \times 10^8}{1.5} \times 1 \times 10^{-9} \\
\mathrm{~d}=0.2 \mathrm{~m}=20 \mathrm{~cm}
\end{aligned}$
Tripura-27.04.2022
Ray Optics
282096
Light enters from air into a given medium at an angle of $45^{\circ}$ with interface of the airmedium surface. After refraction, the light ray is deviated through an angle of $15^{\circ}$ from its original direction. The refractive index of the medium is:
1 1.732
2 1.333
3 1.414
4 2.732
Explanation:
C: Given, incidence angle (i) $=45^{\circ}$, deviation $(\delta)$ $=15^{\circ}$

We know that,
$\begin{aligned}
\delta=i-r \\
r=45^{\circ}-15^{\circ} \\
r=30^{\circ}
\end{aligned}$
From Snell's law, refractive index of medium
$\begin{aligned}
\mu=\frac{\sin i}{\sin r} \\
\mu=\frac{\sin 45^{\circ}}{\sin 30^{\circ}} \\
\mu=\frac{1}{\sqrt{2}} \times \frac{2}{1} \\
\mu=\sqrt{2}=1.414
\end{aligned}$
282092
An optician prescribes a corrective lens of power $+2 \mathrm{D}$, then the focal length of the required convex lens is-
1 $10 \mathrm{~cm}$
2 $50 \mathrm{~cm}$
3 $10 \mathrm{~m}$
4 $50 \mathrm{~m}$
Explanation:
B: Given that, Power of lens $(\mathrm{P})=+2 \mathrm{D}$
Focal length $(f)=\frac{100}{P}$
$\begin{aligned}
f=\frac{100}{2} \\
f=50 \mathrm{~cm}
\end{aligned}$
AP EAMCET-07.07.2022
Ray Optics
282093
A ray of light is incident at $30^{\circ}$ from a medium of refractive index 2 into a medium of refractive index 1 . Then the angle of refraction is
1 $30^{\circ}$
2 $60^0$
3 $45^{\circ}$
4 $90^{\circ}$
Explanation:
D: Given that,
Angle of Incidence $i=30^{\circ}, \mu_1=2, \mu_2=1$
We know that,
$\begin{aligned}
\mu_1 \sin i=\mu_2 \sin r \\
2 \times \sin 30^{\circ}=1 \times \sin r \\
\sin r=\frac{2}{2}=1 \\
\quad r=\sin ^{-1}(1)=90^{\circ}
\end{aligned}$
AP EAMCET-05.07.2022
Ray Optics
282094
A beam of light both reflects and refracts at the surface between air and glass. The index of refraction of the glass is $\mathbf{1 . 4}$. If the refracted and the reflected rays are perpendicular to each other. Then the angle of incidence in the air is.
1 $\tan ^{-1}(1.4)$
2 $\sin ^{-1}\left(\frac{1}{1.4}\right)$
3 $\tan ^{-1}\left(\frac{1}{1.4}\right)$
4 $\sin ^{-1}\left(\frac{1.4}{\pi}\right)$
Explanation:
A: Given that,
Refractive index of glass $\mu_{\mathrm{g}}=1.4$
$\begin{array}{ll}
180^{\circ}=\mathrm{i}+\mathrm{r}+90^{\circ} \\
\therefore \quad & (\mathrm{i}+\mathrm{r})=90^{\circ}
\end{array}$
We know that,
$\begin{aligned}
\mu_a \sin i=\mu_g \sin r \\
1 \times \sin i=1.4 \times \sin (90-i) \\
\frac{\sin i}{\cos i}=1.4 \\
\tan i=1.4 \\
\quad i=\tan ^{-1}(1.4)
\end{aligned}$
AP EAMCET-05.07.2022
Ray Optics
282095
The distance travelled by a light ray in $1 \mathrm{~ns}$ in a glass of refractive index $\mu=1.5$ is
1 $45 \mathrm{~cm}$
2 $40 \mathrm{~cm}$
3 $30 \mathrm{~cm}$
4 $20 \mathrm{~cm}$
Explanation:
D: Given that,
Time $(\mathrm{t})=1 \mathrm{~ns}=10^{-9} \mathrm{~s}$
Refractive index $(\mu)=1.5$
Distance $(d)=$ velocity $\times$ time
$\begin{aligned}
\mathrm{d}=\frac{\mathrm{c}}{\mu} \times \mathrm{t} \\
\mathrm{d}=\frac{3 \times 10^8}{1.5} \times 1 \times 10^{-9} \\
\mathrm{~d}=0.2 \mathrm{~m}=20 \mathrm{~cm}
\end{aligned}$
Tripura-27.04.2022
Ray Optics
282096
Light enters from air into a given medium at an angle of $45^{\circ}$ with interface of the airmedium surface. After refraction, the light ray is deviated through an angle of $15^{\circ}$ from its original direction. The refractive index of the medium is:
1 1.732
2 1.333
3 1.414
4 2.732
Explanation:
C: Given, incidence angle (i) $=45^{\circ}$, deviation $(\delta)$ $=15^{\circ}$

We know that,
$\begin{aligned}
\delta=i-r \\
r=45^{\circ}-15^{\circ} \\
r=30^{\circ}
\end{aligned}$
From Snell's law, refractive index of medium
$\begin{aligned}
\mu=\frac{\sin i}{\sin r} \\
\mu=\frac{\sin 45^{\circ}}{\sin 30^{\circ}} \\
\mu=\frac{1}{\sqrt{2}} \times \frac{2}{1} \\
\mu=\sqrt{2}=1.414
\end{aligned}$
282092
An optician prescribes a corrective lens of power $+2 \mathrm{D}$, then the focal length of the required convex lens is-
1 $10 \mathrm{~cm}$
2 $50 \mathrm{~cm}$
3 $10 \mathrm{~m}$
4 $50 \mathrm{~m}$
Explanation:
B: Given that, Power of lens $(\mathrm{P})=+2 \mathrm{D}$
Focal length $(f)=\frac{100}{P}$
$\begin{aligned}
f=\frac{100}{2} \\
f=50 \mathrm{~cm}
\end{aligned}$
AP EAMCET-07.07.2022
Ray Optics
282093
A ray of light is incident at $30^{\circ}$ from a medium of refractive index 2 into a medium of refractive index 1 . Then the angle of refraction is
1 $30^{\circ}$
2 $60^0$
3 $45^{\circ}$
4 $90^{\circ}$
Explanation:
D: Given that,
Angle of Incidence $i=30^{\circ}, \mu_1=2, \mu_2=1$
We know that,
$\begin{aligned}
\mu_1 \sin i=\mu_2 \sin r \\
2 \times \sin 30^{\circ}=1 \times \sin r \\
\sin r=\frac{2}{2}=1 \\
\quad r=\sin ^{-1}(1)=90^{\circ}
\end{aligned}$
AP EAMCET-05.07.2022
Ray Optics
282094
A beam of light both reflects and refracts at the surface between air and glass. The index of refraction of the glass is $\mathbf{1 . 4}$. If the refracted and the reflected rays are perpendicular to each other. Then the angle of incidence in the air is.
1 $\tan ^{-1}(1.4)$
2 $\sin ^{-1}\left(\frac{1}{1.4}\right)$
3 $\tan ^{-1}\left(\frac{1}{1.4}\right)$
4 $\sin ^{-1}\left(\frac{1.4}{\pi}\right)$
Explanation:
A: Given that,
Refractive index of glass $\mu_{\mathrm{g}}=1.4$
$\begin{array}{ll}
180^{\circ}=\mathrm{i}+\mathrm{r}+90^{\circ} \\
\therefore \quad & (\mathrm{i}+\mathrm{r})=90^{\circ}
\end{array}$
We know that,
$\begin{aligned}
\mu_a \sin i=\mu_g \sin r \\
1 \times \sin i=1.4 \times \sin (90-i) \\
\frac{\sin i}{\cos i}=1.4 \\
\tan i=1.4 \\
\quad i=\tan ^{-1}(1.4)
\end{aligned}$
AP EAMCET-05.07.2022
Ray Optics
282095
The distance travelled by a light ray in $1 \mathrm{~ns}$ in a glass of refractive index $\mu=1.5$ is
1 $45 \mathrm{~cm}$
2 $40 \mathrm{~cm}$
3 $30 \mathrm{~cm}$
4 $20 \mathrm{~cm}$
Explanation:
D: Given that,
Time $(\mathrm{t})=1 \mathrm{~ns}=10^{-9} \mathrm{~s}$
Refractive index $(\mu)=1.5$
Distance $(d)=$ velocity $\times$ time
$\begin{aligned}
\mathrm{d}=\frac{\mathrm{c}}{\mu} \times \mathrm{t} \\
\mathrm{d}=\frac{3 \times 10^8}{1.5} \times 1 \times 10^{-9} \\
\mathrm{~d}=0.2 \mathrm{~m}=20 \mathrm{~cm}
\end{aligned}$
Tripura-27.04.2022
Ray Optics
282096
Light enters from air into a given medium at an angle of $45^{\circ}$ with interface of the airmedium surface. After refraction, the light ray is deviated through an angle of $15^{\circ}$ from its original direction. The refractive index of the medium is:
1 1.732
2 1.333
3 1.414
4 2.732
Explanation:
C: Given, incidence angle (i) $=45^{\circ}$, deviation $(\delta)$ $=15^{\circ}$

We know that,
$\begin{aligned}
\delta=i-r \\
r=45^{\circ}-15^{\circ} \\
r=30^{\circ}
\end{aligned}$
From Snell's law, refractive index of medium
$\begin{aligned}
\mu=\frac{\sin i}{\sin r} \\
\mu=\frac{\sin 45^{\circ}}{\sin 30^{\circ}} \\
\mu=\frac{1}{\sqrt{2}} \times \frac{2}{1} \\
\mu=\sqrt{2}=1.414
\end{aligned}$
282092
An optician prescribes a corrective lens of power $+2 \mathrm{D}$, then the focal length of the required convex lens is-
1 $10 \mathrm{~cm}$
2 $50 \mathrm{~cm}$
3 $10 \mathrm{~m}$
4 $50 \mathrm{~m}$
Explanation:
B: Given that, Power of lens $(\mathrm{P})=+2 \mathrm{D}$
Focal length $(f)=\frac{100}{P}$
$\begin{aligned}
f=\frac{100}{2} \\
f=50 \mathrm{~cm}
\end{aligned}$
AP EAMCET-07.07.2022
Ray Optics
282093
A ray of light is incident at $30^{\circ}$ from a medium of refractive index 2 into a medium of refractive index 1 . Then the angle of refraction is
1 $30^{\circ}$
2 $60^0$
3 $45^{\circ}$
4 $90^{\circ}$
Explanation:
D: Given that,
Angle of Incidence $i=30^{\circ}, \mu_1=2, \mu_2=1$
We know that,
$\begin{aligned}
\mu_1 \sin i=\mu_2 \sin r \\
2 \times \sin 30^{\circ}=1 \times \sin r \\
\sin r=\frac{2}{2}=1 \\
\quad r=\sin ^{-1}(1)=90^{\circ}
\end{aligned}$
AP EAMCET-05.07.2022
Ray Optics
282094
A beam of light both reflects and refracts at the surface between air and glass. The index of refraction of the glass is $\mathbf{1 . 4}$. If the refracted and the reflected rays are perpendicular to each other. Then the angle of incidence in the air is.
1 $\tan ^{-1}(1.4)$
2 $\sin ^{-1}\left(\frac{1}{1.4}\right)$
3 $\tan ^{-1}\left(\frac{1}{1.4}\right)$
4 $\sin ^{-1}\left(\frac{1.4}{\pi}\right)$
Explanation:
A: Given that,
Refractive index of glass $\mu_{\mathrm{g}}=1.4$
$\begin{array}{ll}
180^{\circ}=\mathrm{i}+\mathrm{r}+90^{\circ} \\
\therefore \quad & (\mathrm{i}+\mathrm{r})=90^{\circ}
\end{array}$
We know that,
$\begin{aligned}
\mu_a \sin i=\mu_g \sin r \\
1 \times \sin i=1.4 \times \sin (90-i) \\
\frac{\sin i}{\cos i}=1.4 \\
\tan i=1.4 \\
\quad i=\tan ^{-1}(1.4)
\end{aligned}$
AP EAMCET-05.07.2022
Ray Optics
282095
The distance travelled by a light ray in $1 \mathrm{~ns}$ in a glass of refractive index $\mu=1.5$ is
1 $45 \mathrm{~cm}$
2 $40 \mathrm{~cm}$
3 $30 \mathrm{~cm}$
4 $20 \mathrm{~cm}$
Explanation:
D: Given that,
Time $(\mathrm{t})=1 \mathrm{~ns}=10^{-9} \mathrm{~s}$
Refractive index $(\mu)=1.5$
Distance $(d)=$ velocity $\times$ time
$\begin{aligned}
\mathrm{d}=\frac{\mathrm{c}}{\mu} \times \mathrm{t} \\
\mathrm{d}=\frac{3 \times 10^8}{1.5} \times 1 \times 10^{-9} \\
\mathrm{~d}=0.2 \mathrm{~m}=20 \mathrm{~cm}
\end{aligned}$
Tripura-27.04.2022
Ray Optics
282096
Light enters from air into a given medium at an angle of $45^{\circ}$ with interface of the airmedium surface. After refraction, the light ray is deviated through an angle of $15^{\circ}$ from its original direction. The refractive index of the medium is:
1 1.732
2 1.333
3 1.414
4 2.732
Explanation:
C: Given, incidence angle (i) $=45^{\circ}$, deviation $(\delta)$ $=15^{\circ}$

We know that,
$\begin{aligned}
\delta=i-r \\
r=45^{\circ}-15^{\circ} \\
r=30^{\circ}
\end{aligned}$
From Snell's law, refractive index of medium
$\begin{aligned}
\mu=\frac{\sin i}{\sin r} \\
\mu=\frac{\sin 45^{\circ}}{\sin 30^{\circ}} \\
\mu=\frac{1}{\sqrt{2}} \times \frac{2}{1} \\
\mu=\sqrt{2}=1.414
\end{aligned}$