282018
An object is placed in front of a spherical concave mirror between the focal point and the radius of curvature. Its image is
1 Inverted, real, farther than radius of curvature from mirror
2 Inverted, virtual, closer than focal point to mirror
3 Upright, real, farther than radius of curvature from mirror
4 Inverted, Real, closer than radius of curvature to mirror
Explanation:
A:
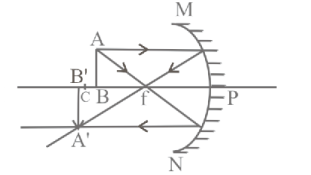
Hence, real image is formed beyond the centre of curvature and image is inverted.
TS EAMCET 05.08.2021
Ray Optics
282019
A linear object of length of $0.1 \mathrm{~m}$ is placed along the axis of a concave mirror of focal length $0.1 \mathrm{~m}$, so that its center lies at the center of curvature. The length of the image formed is
1 $0.13 \mathrm{~m}$
2 $0.17 \mathrm{~m}$
3 $0.3 \mathrm{~m}$
4 $0.2 \mathrm{~m}$
Explanation:
A: Given that, focal length of mirror (f) $=-0.1 \mathrm{~m}$ $=-10 \mathrm{~cm}$
Length of object $=0.1 \mathrm{~m}=10 \mathrm{~cm}$
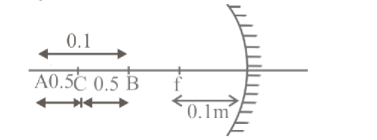
For point B
Distance of object $\left(\mathrm{u}_1\right)=0.1+0.5$
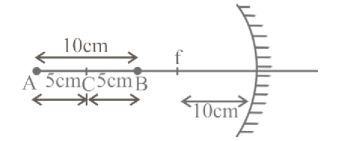
For point B
Distance of object $\left(\mathrm{u}_1\right)=-15 \mathrm{~cm}$
Then, from mirror formula,
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}_1}+\frac{1}{\mathrm{v}_1} \\
-\frac{1}{10}=-\frac{1}{15}+\frac{1}{\mathrm{v}_1} \\
\frac{1}{\mathrm{v}_1}=\frac{1}{15}-\frac{1}{10} \\
\frac{1}{\mathrm{~V}}=\frac{2-3}{30} \\
\mathrm{v}=-30 \mathrm{~cm}
\end{aligned}$
Hence, image at distance $30 \mathrm{~cm}$
For point $\mathrm{A}$
Distance of object $\left(\mathrm{u}_2\right)=-25 \mathrm{~cm}$
Then, from mirror formula
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}_2}+\frac{1}{\mathrm{v}_2} \\
\frac{1}{\mathrm{v}_2}=\frac{1}{25}-\frac{1}{10} \\
\frac{1}{\mathrm{v}_2}=\frac{2-5}{50} \\
\mathrm{v}_2=-\frac{50}{3} \mathrm{~cm}
\end{aligned}$
Hence, image distance at $\frac{50}{3} \mathrm{~cm}$
Then, length of image $=v_1-v_2$
$\begin{aligned}
= & 30-\frac{50}{3} \\
= & \frac{40}{3}=13.33 \mathrm{~cm} \text { or } 0.13 \mathrm{~m}
\end{aligned}$
AP EAMCET-25.09.2020
Ray Optics
282020
An object is placed on the principal axis of a concave mirror at a distance of $1.5 \mathrm{f}$ ( $f$ is the focal length). The image will be at
282021
The size of an image produced by a concave mirror is 4.5 times that of the object. If the object distance is $20 \mathrm{~cm}$, focal length of the mirror is
1 $\frac{90}{11} \mathrm{~cm}$
2 $\frac{120}{11} \mathrm{~cm}$
3 $\frac{150}{11} \mathrm{~cm}$
4 $\frac{180}{11} \mathrm{~cm}$
Explanation:
D: Given, object distance (u) $=-20 \mathrm{~cm}$ Magnification $(\mathrm{m})=-4.5$
We know that,
$\begin{aligned}
\text { Magnification }(\mathrm{m}) & =\frac{-\mathrm{v}}{\mathrm{u}} \\
-4.5 & =\frac{-\mathrm{v}}{-20} \\
\mathrm{v} & =-90 \mathrm{~cm}
\end{aligned}$
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{f}}=-\frac{1}{20}-\frac{1}{90} \\
\frac{1}{\mathrm{f}}=\frac{-9-2}{180} \\
\mathrm{f}=-\frac{180}{11} \mathrm{~cm}
\end{aligned}$
Hence, focal length of the mirror is $\frac{180}{11}$.
282018
An object is placed in front of a spherical concave mirror between the focal point and the radius of curvature. Its image is
1 Inverted, real, farther than radius of curvature from mirror
2 Inverted, virtual, closer than focal point to mirror
3 Upright, real, farther than radius of curvature from mirror
4 Inverted, Real, closer than radius of curvature to mirror
Explanation:
A:

Hence, real image is formed beyond the centre of curvature and image is inverted.
TS EAMCET 05.08.2021
Ray Optics
282019
A linear object of length of $0.1 \mathrm{~m}$ is placed along the axis of a concave mirror of focal length $0.1 \mathrm{~m}$, so that its center lies at the center of curvature. The length of the image formed is
1 $0.13 \mathrm{~m}$
2 $0.17 \mathrm{~m}$
3 $0.3 \mathrm{~m}$
4 $0.2 \mathrm{~m}$
Explanation:
A: Given that, focal length of mirror (f) $=-0.1 \mathrm{~m}$ $=-10 \mathrm{~cm}$
Length of object $=0.1 \mathrm{~m}=10 \mathrm{~cm}$

For point B
Distance of object $\left(\mathrm{u}_1\right)=0.1+0.5$

For point B
Distance of object $\left(\mathrm{u}_1\right)=-15 \mathrm{~cm}$
Then, from mirror formula,
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}_1}+\frac{1}{\mathrm{v}_1} \\
-\frac{1}{10}=-\frac{1}{15}+\frac{1}{\mathrm{v}_1} \\
\frac{1}{\mathrm{v}_1}=\frac{1}{15}-\frac{1}{10} \\
\frac{1}{\mathrm{~V}}=\frac{2-3}{30} \\
\mathrm{v}=-30 \mathrm{~cm}
\end{aligned}$
Hence, image at distance $30 \mathrm{~cm}$
For point $\mathrm{A}$
Distance of object $\left(\mathrm{u}_2\right)=-25 \mathrm{~cm}$
Then, from mirror formula
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}_2}+\frac{1}{\mathrm{v}_2} \\
\frac{1}{\mathrm{v}_2}=\frac{1}{25}-\frac{1}{10} \\
\frac{1}{\mathrm{v}_2}=\frac{2-5}{50} \\
\mathrm{v}_2=-\frac{50}{3} \mathrm{~cm}
\end{aligned}$
Hence, image distance at $\frac{50}{3} \mathrm{~cm}$
Then, length of image $=v_1-v_2$
$\begin{aligned}
= & 30-\frac{50}{3} \\
= & \frac{40}{3}=13.33 \mathrm{~cm} \text { or } 0.13 \mathrm{~m}
\end{aligned}$
AP EAMCET-25.09.2020
Ray Optics
282020
An object is placed on the principal axis of a concave mirror at a distance of $1.5 \mathrm{f}$ ( $f$ is the focal length). The image will be at
282021
The size of an image produced by a concave mirror is 4.5 times that of the object. If the object distance is $20 \mathrm{~cm}$, focal length of the mirror is
1 $\frac{90}{11} \mathrm{~cm}$
2 $\frac{120}{11} \mathrm{~cm}$
3 $\frac{150}{11} \mathrm{~cm}$
4 $\frac{180}{11} \mathrm{~cm}$
Explanation:
D: Given, object distance (u) $=-20 \mathrm{~cm}$ Magnification $(\mathrm{m})=-4.5$
We know that,
$\begin{aligned}
\text { Magnification }(\mathrm{m}) & =\frac{-\mathrm{v}}{\mathrm{u}} \\
-4.5 & =\frac{-\mathrm{v}}{-20} \\
\mathrm{v} & =-90 \mathrm{~cm}
\end{aligned}$
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{f}}=-\frac{1}{20}-\frac{1}{90} \\
\frac{1}{\mathrm{f}}=\frac{-9-2}{180} \\
\mathrm{f}=-\frac{180}{11} \mathrm{~cm}
\end{aligned}$
Hence, focal length of the mirror is $\frac{180}{11}$.
282018
An object is placed in front of a spherical concave mirror between the focal point and the radius of curvature. Its image is
1 Inverted, real, farther than radius of curvature from mirror
2 Inverted, virtual, closer than focal point to mirror
3 Upright, real, farther than radius of curvature from mirror
4 Inverted, Real, closer than radius of curvature to mirror
Explanation:
A:

Hence, real image is formed beyond the centre of curvature and image is inverted.
TS EAMCET 05.08.2021
Ray Optics
282019
A linear object of length of $0.1 \mathrm{~m}$ is placed along the axis of a concave mirror of focal length $0.1 \mathrm{~m}$, so that its center lies at the center of curvature. The length of the image formed is
1 $0.13 \mathrm{~m}$
2 $0.17 \mathrm{~m}$
3 $0.3 \mathrm{~m}$
4 $0.2 \mathrm{~m}$
Explanation:
A: Given that, focal length of mirror (f) $=-0.1 \mathrm{~m}$ $=-10 \mathrm{~cm}$
Length of object $=0.1 \mathrm{~m}=10 \mathrm{~cm}$

For point B
Distance of object $\left(\mathrm{u}_1\right)=0.1+0.5$

For point B
Distance of object $\left(\mathrm{u}_1\right)=-15 \mathrm{~cm}$
Then, from mirror formula,
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}_1}+\frac{1}{\mathrm{v}_1} \\
-\frac{1}{10}=-\frac{1}{15}+\frac{1}{\mathrm{v}_1} \\
\frac{1}{\mathrm{v}_1}=\frac{1}{15}-\frac{1}{10} \\
\frac{1}{\mathrm{~V}}=\frac{2-3}{30} \\
\mathrm{v}=-30 \mathrm{~cm}
\end{aligned}$
Hence, image at distance $30 \mathrm{~cm}$
For point $\mathrm{A}$
Distance of object $\left(\mathrm{u}_2\right)=-25 \mathrm{~cm}$
Then, from mirror formula
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}_2}+\frac{1}{\mathrm{v}_2} \\
\frac{1}{\mathrm{v}_2}=\frac{1}{25}-\frac{1}{10} \\
\frac{1}{\mathrm{v}_2}=\frac{2-5}{50} \\
\mathrm{v}_2=-\frac{50}{3} \mathrm{~cm}
\end{aligned}$
Hence, image distance at $\frac{50}{3} \mathrm{~cm}$
Then, length of image $=v_1-v_2$
$\begin{aligned}
= & 30-\frac{50}{3} \\
= & \frac{40}{3}=13.33 \mathrm{~cm} \text { or } 0.13 \mathrm{~m}
\end{aligned}$
AP EAMCET-25.09.2020
Ray Optics
282020
An object is placed on the principal axis of a concave mirror at a distance of $1.5 \mathrm{f}$ ( $f$ is the focal length). The image will be at
282021
The size of an image produced by a concave mirror is 4.5 times that of the object. If the object distance is $20 \mathrm{~cm}$, focal length of the mirror is
1 $\frac{90}{11} \mathrm{~cm}$
2 $\frac{120}{11} \mathrm{~cm}$
3 $\frac{150}{11} \mathrm{~cm}$
4 $\frac{180}{11} \mathrm{~cm}$
Explanation:
D: Given, object distance (u) $=-20 \mathrm{~cm}$ Magnification $(\mathrm{m})=-4.5$
We know that,
$\begin{aligned}
\text { Magnification }(\mathrm{m}) & =\frac{-\mathrm{v}}{\mathrm{u}} \\
-4.5 & =\frac{-\mathrm{v}}{-20} \\
\mathrm{v} & =-90 \mathrm{~cm}
\end{aligned}$
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{f}}=-\frac{1}{20}-\frac{1}{90} \\
\frac{1}{\mathrm{f}}=\frac{-9-2}{180} \\
\mathrm{f}=-\frac{180}{11} \mathrm{~cm}
\end{aligned}$
Hence, focal length of the mirror is $\frac{180}{11}$.
282018
An object is placed in front of a spherical concave mirror between the focal point and the radius of curvature. Its image is
1 Inverted, real, farther than radius of curvature from mirror
2 Inverted, virtual, closer than focal point to mirror
3 Upright, real, farther than radius of curvature from mirror
4 Inverted, Real, closer than radius of curvature to mirror
Explanation:
A:

Hence, real image is formed beyond the centre of curvature and image is inverted.
TS EAMCET 05.08.2021
Ray Optics
282019
A linear object of length of $0.1 \mathrm{~m}$ is placed along the axis of a concave mirror of focal length $0.1 \mathrm{~m}$, so that its center lies at the center of curvature. The length of the image formed is
1 $0.13 \mathrm{~m}$
2 $0.17 \mathrm{~m}$
3 $0.3 \mathrm{~m}$
4 $0.2 \mathrm{~m}$
Explanation:
A: Given that, focal length of mirror (f) $=-0.1 \mathrm{~m}$ $=-10 \mathrm{~cm}$
Length of object $=0.1 \mathrm{~m}=10 \mathrm{~cm}$

For point B
Distance of object $\left(\mathrm{u}_1\right)=0.1+0.5$

For point B
Distance of object $\left(\mathrm{u}_1\right)=-15 \mathrm{~cm}$
Then, from mirror formula,
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}_1}+\frac{1}{\mathrm{v}_1} \\
-\frac{1}{10}=-\frac{1}{15}+\frac{1}{\mathrm{v}_1} \\
\frac{1}{\mathrm{v}_1}=\frac{1}{15}-\frac{1}{10} \\
\frac{1}{\mathrm{~V}}=\frac{2-3}{30} \\
\mathrm{v}=-30 \mathrm{~cm}
\end{aligned}$
Hence, image at distance $30 \mathrm{~cm}$
For point $\mathrm{A}$
Distance of object $\left(\mathrm{u}_2\right)=-25 \mathrm{~cm}$
Then, from mirror formula
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}_2}+\frac{1}{\mathrm{v}_2} \\
\frac{1}{\mathrm{v}_2}=\frac{1}{25}-\frac{1}{10} \\
\frac{1}{\mathrm{v}_2}=\frac{2-5}{50} \\
\mathrm{v}_2=-\frac{50}{3} \mathrm{~cm}
\end{aligned}$
Hence, image distance at $\frac{50}{3} \mathrm{~cm}$
Then, length of image $=v_1-v_2$
$\begin{aligned}
= & 30-\frac{50}{3} \\
= & \frac{40}{3}=13.33 \mathrm{~cm} \text { or } 0.13 \mathrm{~m}
\end{aligned}$
AP EAMCET-25.09.2020
Ray Optics
282020
An object is placed on the principal axis of a concave mirror at a distance of $1.5 \mathrm{f}$ ( $f$ is the focal length). The image will be at
282021
The size of an image produced by a concave mirror is 4.5 times that of the object. If the object distance is $20 \mathrm{~cm}$, focal length of the mirror is
1 $\frac{90}{11} \mathrm{~cm}$
2 $\frac{120}{11} \mathrm{~cm}$
3 $\frac{150}{11} \mathrm{~cm}$
4 $\frac{180}{11} \mathrm{~cm}$
Explanation:
D: Given, object distance (u) $=-20 \mathrm{~cm}$ Magnification $(\mathrm{m})=-4.5$
We know that,
$\begin{aligned}
\text { Magnification }(\mathrm{m}) & =\frac{-\mathrm{v}}{\mathrm{u}} \\
-4.5 & =\frac{-\mathrm{v}}{-20} \\
\mathrm{v} & =-90 \mathrm{~cm}
\end{aligned}$
From mirror formula -
$\begin{aligned}
\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \\
\frac{1}{\mathrm{f}}=-\frac{1}{20}-\frac{1}{90} \\
\frac{1}{\mathrm{f}}=\frac{-9-2}{180} \\
\mathrm{f}=-\frac{180}{11} \mathrm{~cm}
\end{aligned}$
Hence, focal length of the mirror is $\frac{180}{11}$.