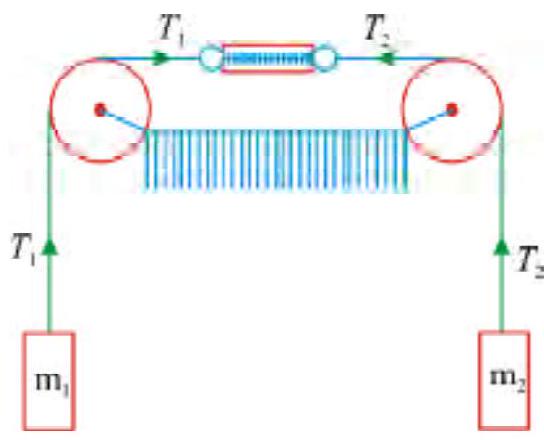
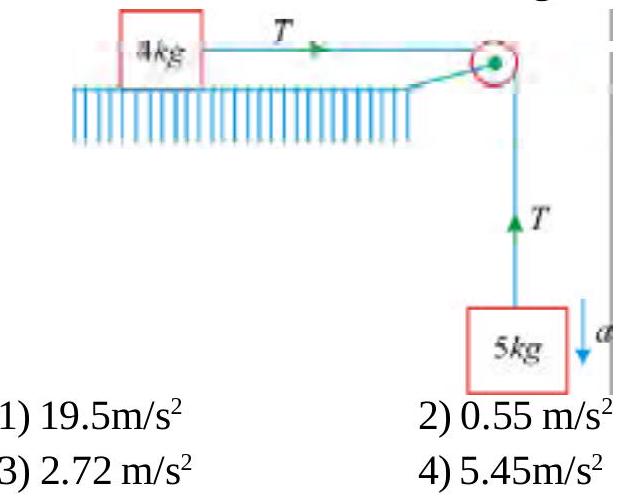
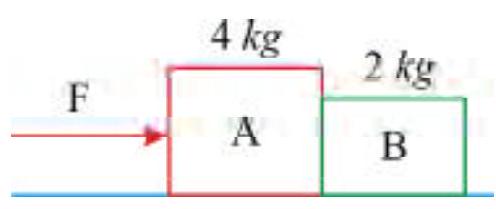
270155 A horizontal force \(F\) pushes a \(4 \mathrm{~kg}\) block (A) which pushes against a \(2 \mathrm{~kg}\) block (B) as shown. The blocks have an acceleration of \(3 \mathrm{~m} / \mathrm{s}^{2}\) to the right. There is no friction between the blocks and the surfaces on which they slide. What is the net force \(B\) exerts on \(A\) ?

270156 Two masses \(m_{1}\) and \(m_{2}\) are attached to a spring balance \(S\) as shown in Figure. If \(m_{1}\lt m_{2}\) then the reading of spring balance will be

270157 Two masses \((M+m)\) and \((M-m)\) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is

270158 Two bodies of masses \(5 \mathrm{~kg}\) and \(4 \mathrm{~kg}\) are tied to a string as shown. If the table and pulley are smooth, then acceleration of \(5 \mathrm{~kg}\) mass will be

270155 A horizontal force \(F\) pushes a \(4 \mathrm{~kg}\) block (A) which pushes against a \(2 \mathrm{~kg}\) block (B) as shown. The blocks have an acceleration of \(3 \mathrm{~m} / \mathrm{s}^{2}\) to the right. There is no friction between the blocks and the surfaces on which they slide. What is the net force \(B\) exerts on \(A\) ?

270156 Two masses \(m_{1}\) and \(m_{2}\) are attached to a spring balance \(S\) as shown in Figure. If \(m_{1}\lt m_{2}\) then the reading of spring balance will be

270157 Two masses \((M+m)\) and \((M-m)\) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is

270158 Two bodies of masses \(5 \mathrm{~kg}\) and \(4 \mathrm{~kg}\) are tied to a string as shown. If the table and pulley are smooth, then acceleration of \(5 \mathrm{~kg}\) mass will be

270155 A horizontal force \(F\) pushes a \(4 \mathrm{~kg}\) block (A) which pushes against a \(2 \mathrm{~kg}\) block (B) as shown. The blocks have an acceleration of \(3 \mathrm{~m} / \mathrm{s}^{2}\) to the right. There is no friction between the blocks and the surfaces on which they slide. What is the net force \(B\) exerts on \(A\) ?

270156 Two masses \(m_{1}\) and \(m_{2}\) are attached to a spring balance \(S\) as shown in Figure. If \(m_{1}\lt m_{2}\) then the reading of spring balance will be

270157 Two masses \((M+m)\) and \((M-m)\) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is

270158 Two bodies of masses \(5 \mathrm{~kg}\) and \(4 \mathrm{~kg}\) are tied to a string as shown. If the table and pulley are smooth, then acceleration of \(5 \mathrm{~kg}\) mass will be

270155 A horizontal force \(F\) pushes a \(4 \mathrm{~kg}\) block (A) which pushes against a \(2 \mathrm{~kg}\) block (B) as shown. The blocks have an acceleration of \(3 \mathrm{~m} / \mathrm{s}^{2}\) to the right. There is no friction between the blocks and the surfaces on which they slide. What is the net force \(B\) exerts on \(A\) ?

270156 Two masses \(m_{1}\) and \(m_{2}\) are attached to a spring balance \(S\) as shown in Figure. If \(m_{1}\lt m_{2}\) then the reading of spring balance will be

270157 Two masses \((M+m)\) and \((M-m)\) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is

270158 Two bodies of masses \(5 \mathrm{~kg}\) and \(4 \mathrm{~kg}\) are tied to a string as shown. If the table and pulley are smooth, then acceleration of \(5 \mathrm{~kg}\) mass will be