270152 A person of mass \(60 \mathrm{~kg}\) is in a lift. The change in the apparent weight of the person, when the lift moves up with an acceleration of \(2 \mathrm{~ms}^{-2}\) and then down with an acceleration of \(2 \mathrm{~ms}^{-2}\), is (take \(\mathbf{g}=10 \mathrm{~m} / \mathrm{sec}^{2}\) )
270154
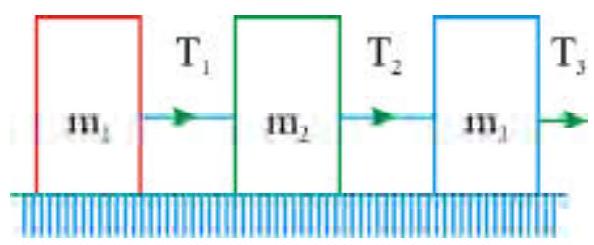
Three blocks of masses \(m_{1}, m_{2}\) and \(m_{3}\) are connected by a massless string as shown in figure on a frictionless table. They are pulled with a force \(\mathbf{T}_{3}=40 \mathrm{~N}\). If \(m_{1}=10 \mathrm{~kg}, m_{2}=6 \mathrm{~kg}\) and \(m_{3}=4 \mathrm{~kg}\), then tension \(\mathrm{T}_{2}\) will be
270152 A person of mass \(60 \mathrm{~kg}\) is in a lift. The change in the apparent weight of the person, when the lift moves up with an acceleration of \(2 \mathrm{~ms}^{-2}\) and then down with an acceleration of \(2 \mathrm{~ms}^{-2}\), is (take \(\mathbf{g}=10 \mathrm{~m} / \mathrm{sec}^{2}\) )
270154
Three blocks of masses \(m_{1}, m_{2}\) and \(m_{3}\) are connected by a massless string as shown in figure on a frictionless table. They are pulled with a force \(\mathbf{T}_{3}=40 \mathrm{~N}\). If \(m_{1}=10 \mathrm{~kg}, m_{2}=6 \mathrm{~kg}\) and \(m_{3}=4 \mathrm{~kg}\), then tension \(\mathrm{T}_{2}\) will be

270152 A person of mass \(60 \mathrm{~kg}\) is in a lift. The change in the apparent weight of the person, when the lift moves up with an acceleration of \(2 \mathrm{~ms}^{-2}\) and then down with an acceleration of \(2 \mathrm{~ms}^{-2}\), is (take \(\mathbf{g}=10 \mathrm{~m} / \mathrm{sec}^{2}\) )
270154
Three blocks of masses \(m_{1}, m_{2}\) and \(m_{3}\) are connected by a massless string as shown in figure on a frictionless table. They are pulled with a force \(\mathbf{T}_{3}=40 \mathrm{~N}\). If \(m_{1}=10 \mathrm{~kg}, m_{2}=6 \mathrm{~kg}\) and \(m_{3}=4 \mathrm{~kg}\), then tension \(\mathrm{T}_{2}\) will be

270152 A person of mass \(60 \mathrm{~kg}\) is in a lift. The change in the apparent weight of the person, when the lift moves up with an acceleration of \(2 \mathrm{~ms}^{-2}\) and then down with an acceleration of \(2 \mathrm{~ms}^{-2}\), is (take \(\mathbf{g}=10 \mathrm{~m} / \mathrm{sec}^{2}\) )
270154
Three blocks of masses \(m_{1}, m_{2}\) and \(m_{3}\) are connected by a massless string as shown in figure on a frictionless table. They are pulled with a force \(\mathbf{T}_{3}=40 \mathrm{~N}\). If \(m_{1}=10 \mathrm{~kg}, m_{2}=6 \mathrm{~kg}\) and \(m_{3}=4 \mathrm{~kg}\), then tension \(\mathrm{T}_{2}\) will be

270152 A person of mass \(60 \mathrm{~kg}\) is in a lift. The change in the apparent weight of the person, when the lift moves up with an acceleration of \(2 \mathrm{~ms}^{-2}\) and then down with an acceleration of \(2 \mathrm{~ms}^{-2}\), is (take \(\mathbf{g}=10 \mathrm{~m} / \mathrm{sec}^{2}\) )
270154
Three blocks of masses \(m_{1}, m_{2}\) and \(m_{3}\) are connected by a massless string as shown in figure on a frictionless table. They are pulled with a force \(\mathbf{T}_{3}=40 \mathrm{~N}\). If \(m_{1}=10 \mathrm{~kg}, m_{2}=6 \mathrm{~kg}\) and \(m_{3}=4 \mathrm{~kg}\), then tension \(\mathrm{T}_{2}\) will be

