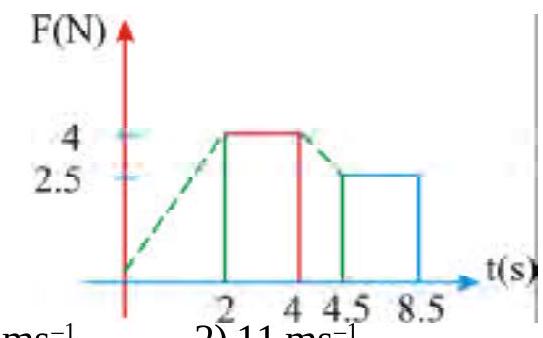
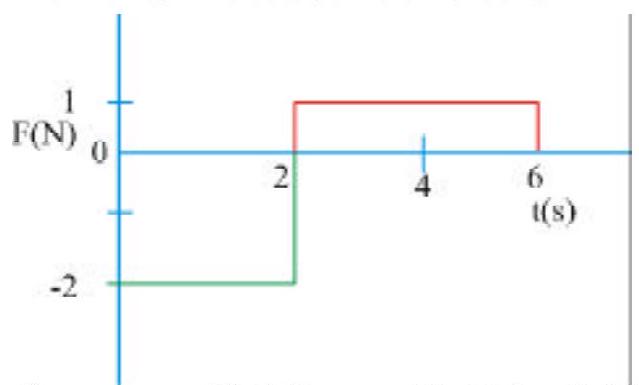
270144 A small sphere of mass \(m=2 \mathrm{~kg}\) moving with a velocity \(\bar{u}=4 \hat{i}-7 \hat{j} \mathrm{~m} / \mathrm{s}\) collides with a smooth wall and returns with a velocity \(\bar{v}=\hat{i}+3 \hat{j} \mathrm{~m} / \mathrm{s}\). The magnitude of the impulse received by the ball is
270144 A small sphere of mass \(m=2 \mathrm{~kg}\) moving with a velocity \(\bar{u}=4 \hat{i}-7 \hat{j} \mathrm{~m} / \mathrm{s}\) collides with a smooth wall and returns with a velocity \(\bar{v}=\hat{i}+3 \hat{j} \mathrm{~m} / \mathrm{s}\). The magnitude of the impulse received by the ball is
270144 A small sphere of mass \(m=2 \mathrm{~kg}\) moving with a velocity \(\bar{u}=4 \hat{i}-7 \hat{j} \mathrm{~m} / \mathrm{s}\) collides with a smooth wall and returns with a velocity \(\bar{v}=\hat{i}+3 \hat{j} \mathrm{~m} / \mathrm{s}\). The magnitude of the impulse received by the ball is
270144 A small sphere of mass \(m=2 \mathrm{~kg}\) moving with a velocity \(\bar{u}=4 \hat{i}-7 \hat{j} \mathrm{~m} / \mathrm{s}\) collides with a smooth wall and returns with a velocity \(\bar{v}=\hat{i}+3 \hat{j} \mathrm{~m} / \mathrm{s}\). The magnitude of the impulse received by the ball is
270144 A small sphere of mass \(m=2 \mathrm{~kg}\) moving with a velocity \(\bar{u}=4 \hat{i}-7 \hat{j} \mathrm{~m} / \mathrm{s}\) collides with a smooth wall and returns with a velocity \(\bar{v}=\hat{i}+3 \hat{j} \mathrm{~m} / \mathrm{s}\). The magnitude of the impulse received by the ball is