269872 A man can row a boat in still water with a velocity of\(8 \mathrm{kmph}\). Water is flowing in a river with a velocity of \(4 \mathrm{kmph}\). At what angle should he row the boat so as to reach the exact opposite point

269873 A person can swim in still water at\(5 \mathrm{~m} / \mathrm{s}\). He moves in a river of velocity \(3 \mathrm{~m} / \mathrm{s}\), first down the stream and next same distance up the stream. The ratio of times taken are

269874 The velocity of water in a river is\(\mathbf{2} \mathbf{~ m m p h}\), while width is \(400 \mathrm{~m}\). A boat is rowed from a point rowing always aiming opposite point at \(8 \mathrm{kmph}\) of still water velocity. On reaching the opposite bank the drift obtained is

269875 A man can swim in still water at a speed of 4\(\mathrm{kmph}\). He desires to cross a river flowing at a speed of \(3 \mathrm{kmph}\) in the shortest time interval. If the width of the river is \(3 \mathrm{~km}\) time taken to cross the river (in hours) and the horizontal distance travelled ( in \(\mathbf{k m}\) ) are respectively

269914 A man can swim in still water at a speed of 6\(\mathrm{kmph}\) and he has to cross the river and reach just opposite point on the other bank. If the river is flowing at a speed of \(3 \mathbf{k m p h}\), and the width of the river is \(2 \mathrm{~km}\), the time taken to cross the river is (in hours)

269872 A man can row a boat in still water with a velocity of\(8 \mathrm{kmph}\). Water is flowing in a river with a velocity of \(4 \mathrm{kmph}\). At what angle should he row the boat so as to reach the exact opposite point

269873 A person can swim in still water at\(5 \mathrm{~m} / \mathrm{s}\). He moves in a river of velocity \(3 \mathrm{~m} / \mathrm{s}\), first down the stream and next same distance up the stream. The ratio of times taken are

269874 The velocity of water in a river is\(\mathbf{2} \mathbf{~ m m p h}\), while width is \(400 \mathrm{~m}\). A boat is rowed from a point rowing always aiming opposite point at \(8 \mathrm{kmph}\) of still water velocity. On reaching the opposite bank the drift obtained is

269875 A man can swim in still water at a speed of 4\(\mathrm{kmph}\). He desires to cross a river flowing at a speed of \(3 \mathrm{kmph}\) in the shortest time interval. If the width of the river is \(3 \mathrm{~km}\) time taken to cross the river (in hours) and the horizontal distance travelled ( in \(\mathbf{k m}\) ) are respectively

269914 A man can swim in still water at a speed of 6\(\mathrm{kmph}\) and he has to cross the river and reach just opposite point on the other bank. If the river is flowing at a speed of \(3 \mathbf{k m p h}\), and the width of the river is \(2 \mathrm{~km}\), the time taken to cross the river is (in hours)

269872 A man can row a boat in still water with a velocity of\(8 \mathrm{kmph}\). Water is flowing in a river with a velocity of \(4 \mathrm{kmph}\). At what angle should he row the boat so as to reach the exact opposite point

269873 A person can swim in still water at\(5 \mathrm{~m} / \mathrm{s}\). He moves in a river of velocity \(3 \mathrm{~m} / \mathrm{s}\), first down the stream and next same distance up the stream. The ratio of times taken are

269874 The velocity of water in a river is\(\mathbf{2} \mathbf{~ m m p h}\), while width is \(400 \mathrm{~m}\). A boat is rowed from a point rowing always aiming opposite point at \(8 \mathrm{kmph}\) of still water velocity. On reaching the opposite bank the drift obtained is

269875 A man can swim in still water at a speed of 4\(\mathrm{kmph}\). He desires to cross a river flowing at a speed of \(3 \mathrm{kmph}\) in the shortest time interval. If the width of the river is \(3 \mathrm{~km}\) time taken to cross the river (in hours) and the horizontal distance travelled ( in \(\mathbf{k m}\) ) are respectively

269914 A man can swim in still water at a speed of 6\(\mathrm{kmph}\) and he has to cross the river and reach just opposite point on the other bank. If the river is flowing at a speed of \(3 \mathbf{k m p h}\), and the width of the river is \(2 \mathrm{~km}\), the time taken to cross the river is (in hours)

269872 A man can row a boat in still water with a velocity of\(8 \mathrm{kmph}\). Water is flowing in a river with a velocity of \(4 \mathrm{kmph}\). At what angle should he row the boat so as to reach the exact opposite point

269873 A person can swim in still water at\(5 \mathrm{~m} / \mathrm{s}\). He moves in a river of velocity \(3 \mathrm{~m} / \mathrm{s}\), first down the stream and next same distance up the stream. The ratio of times taken are

269874 The velocity of water in a river is\(\mathbf{2} \mathbf{~ m m p h}\), while width is \(400 \mathrm{~m}\). A boat is rowed from a point rowing always aiming opposite point at \(8 \mathrm{kmph}\) of still water velocity. On reaching the opposite bank the drift obtained is

269875 A man can swim in still water at a speed of 4\(\mathrm{kmph}\). He desires to cross a river flowing at a speed of \(3 \mathrm{kmph}\) in the shortest time interval. If the width of the river is \(3 \mathrm{~km}\) time taken to cross the river (in hours) and the horizontal distance travelled ( in \(\mathbf{k m}\) ) are respectively

269914 A man can swim in still water at a speed of 6\(\mathrm{kmph}\) and he has to cross the river and reach just opposite point on the other bank. If the river is flowing at a speed of \(3 \mathbf{k m p h}\), and the width of the river is \(2 \mathrm{~km}\), the time taken to cross the river is (in hours)

269872 A man can row a boat in still water with a velocity of\(8 \mathrm{kmph}\). Water is flowing in a river with a velocity of \(4 \mathrm{kmph}\). At what angle should he row the boat so as to reach the exact opposite point

269873 A person can swim in still water at\(5 \mathrm{~m} / \mathrm{s}\). He moves in a river of velocity \(3 \mathrm{~m} / \mathrm{s}\), first down the stream and next same distance up the stream. The ratio of times taken are

269874 The velocity of water in a river is\(\mathbf{2} \mathbf{~ m m p h}\), while width is \(400 \mathrm{~m}\). A boat is rowed from a point rowing always aiming opposite point at \(8 \mathrm{kmph}\) of still water velocity. On reaching the opposite bank the drift obtained is

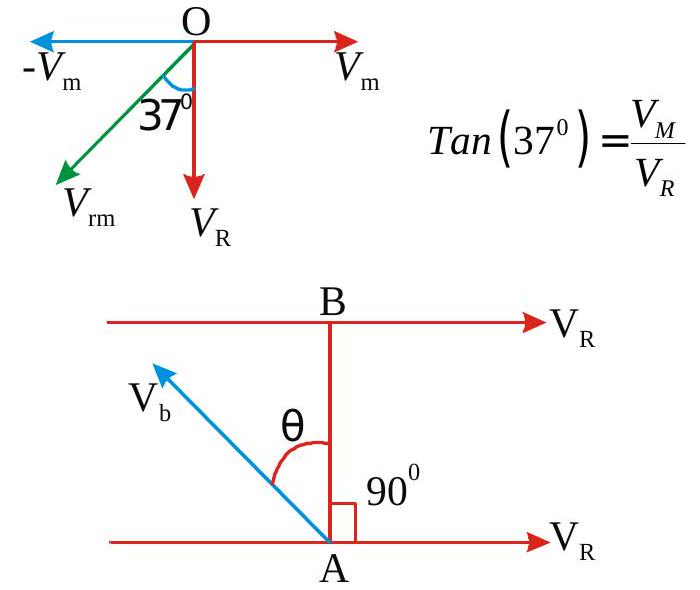
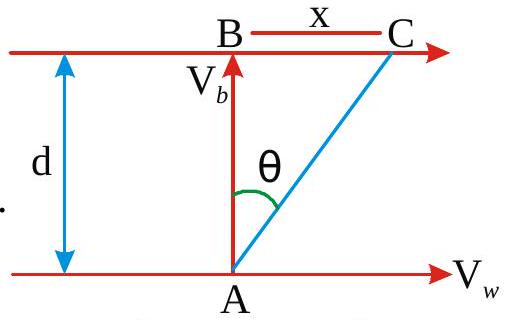
269875 A man can swim in still water at a speed of 4\(\mathrm{kmph}\). He desires to cross a river flowing at a speed of \(3 \mathrm{kmph}\) in the shortest time interval. If the width of the river is \(3 \mathrm{~km}\) time taken to cross the river (in hours) and the horizontal distance travelled ( in \(\mathbf{k m}\) ) are respectively

269914 A man can swim in still water at a speed of 6\(\mathrm{kmph}\) and he has to cross the river and reach just opposite point on the other bank. If the river is flowing at a speed of \(3 \mathbf{k m p h}\), and the width of the river is \(2 \mathrm{~km}\), the time taken to cross the river is (in hours)