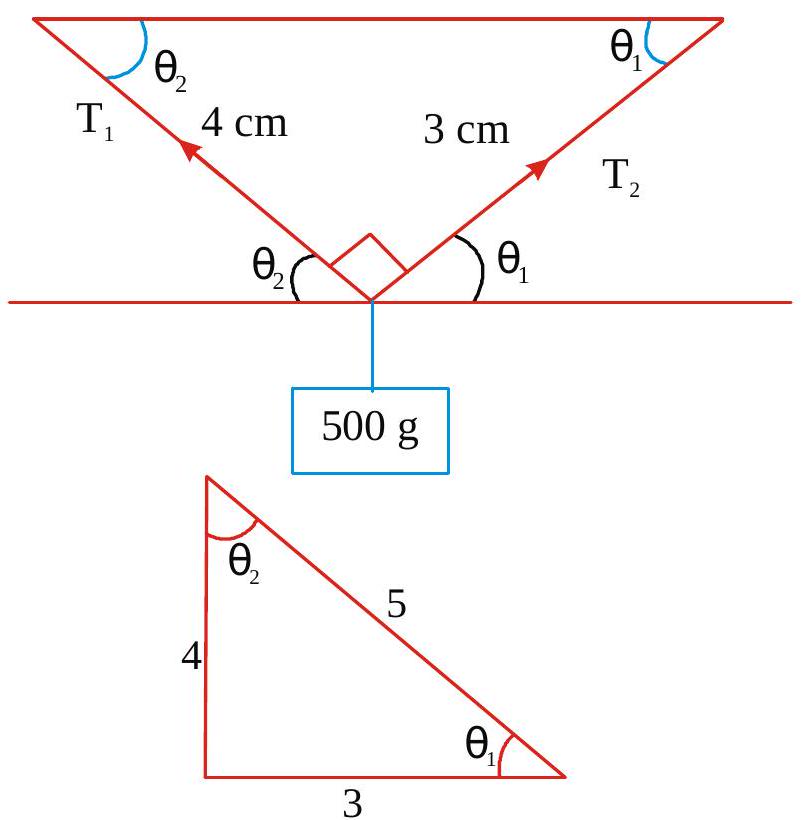
269905 Two light strings of length\(4 \mathrm{~cm}\) and \(3 \mathrm{~cm}\) are tied to a bob of weight \(500 \mathrm{gm}\). The free ends of the strings are tied to pegs in the same horizontal line and separated by \(5 \mathrm{~cm}\).The ratio of tension in the longer string to that in the shorter string is

269939 The greatest and least resultant of two forces acting at a point are \(29 \mathrm{Kg} \mathrm{wt}\). and \(5 \mathrm{Kg} \mathrm{wt}\). respectively. If each force is increased by 3 \(\mathrm{Kg}\) wt. the magnitude of the resultant of new forces acting at right angles to each other is

269940 Two forces \(\mathbf{P}\) and \(\mathbf{Q}\) act at an angle of \(120^{\circ}\) with each other. If the resultant is at right angles to \(P\) and \(P\) is equal to \(4 \mathrm{~kg}\)-wt, then the value of \(Q\) is

269941 The resultant of two vectors \(\vec{P} \& \vec{Q}\) is \(\vec{R}\). If the magnitude of \(\vec{Q}\) is doubled the new resultant becomes perpendicular to \(\overrightarrow{\mathrm{p}}\) then magnitude of \(\vec{R}\) is

269942 \(\quad \vec{P}, \vec{Q}, \vec{R}, \vec{S}\) are vector of equal magnitude. If \(\vec{P}+\vec{Q}-\vec{R}=0\) angle between \(\vec{P}\) and \(\vec{Q}\) is \(\theta_{1}\). If \(\vec{P}+\vec{Q}-\vec{S}=0\) angle between \(\vec{P}\) and \(\vec{S}\) is \(\theta_{2}\). The ratio of \(\theta_{1}\) to \(\theta_{2}\) is

269905 Two light strings of length\(4 \mathrm{~cm}\) and \(3 \mathrm{~cm}\) are tied to a bob of weight \(500 \mathrm{gm}\). The free ends of the strings are tied to pegs in the same horizontal line and separated by \(5 \mathrm{~cm}\).The ratio of tension in the longer string to that in the shorter string is

269939 The greatest and least resultant of two forces acting at a point are \(29 \mathrm{Kg} \mathrm{wt}\). and \(5 \mathrm{Kg} \mathrm{wt}\). respectively. If each force is increased by 3 \(\mathrm{Kg}\) wt. the magnitude of the resultant of new forces acting at right angles to each other is

269940 Two forces \(\mathbf{P}\) and \(\mathbf{Q}\) act at an angle of \(120^{\circ}\) with each other. If the resultant is at right angles to \(P\) and \(P\) is equal to \(4 \mathrm{~kg}\)-wt, then the value of \(Q\) is

269941 The resultant of two vectors \(\vec{P} \& \vec{Q}\) is \(\vec{R}\). If the magnitude of \(\vec{Q}\) is doubled the new resultant becomes perpendicular to \(\overrightarrow{\mathrm{p}}\) then magnitude of \(\vec{R}\) is

269942 \(\quad \vec{P}, \vec{Q}, \vec{R}, \vec{S}\) are vector of equal magnitude. If \(\vec{P}+\vec{Q}-\vec{R}=0\) angle between \(\vec{P}\) and \(\vec{Q}\) is \(\theta_{1}\). If \(\vec{P}+\vec{Q}-\vec{S}=0\) angle between \(\vec{P}\) and \(\vec{S}\) is \(\theta_{2}\). The ratio of \(\theta_{1}\) to \(\theta_{2}\) is

269905 Two light strings of length\(4 \mathrm{~cm}\) and \(3 \mathrm{~cm}\) are tied to a bob of weight \(500 \mathrm{gm}\). The free ends of the strings are tied to pegs in the same horizontal line and separated by \(5 \mathrm{~cm}\).The ratio of tension in the longer string to that in the shorter string is

269939 The greatest and least resultant of two forces acting at a point are \(29 \mathrm{Kg} \mathrm{wt}\). and \(5 \mathrm{Kg} \mathrm{wt}\). respectively. If each force is increased by 3 \(\mathrm{Kg}\) wt. the magnitude of the resultant of new forces acting at right angles to each other is

269940 Two forces \(\mathbf{P}\) and \(\mathbf{Q}\) act at an angle of \(120^{\circ}\) with each other. If the resultant is at right angles to \(P\) and \(P\) is equal to \(4 \mathrm{~kg}\)-wt, then the value of \(Q\) is

269941 The resultant of two vectors \(\vec{P} \& \vec{Q}\) is \(\vec{R}\). If the magnitude of \(\vec{Q}\) is doubled the new resultant becomes perpendicular to \(\overrightarrow{\mathrm{p}}\) then magnitude of \(\vec{R}\) is

269942 \(\quad \vec{P}, \vec{Q}, \vec{R}, \vec{S}\) are vector of equal magnitude. If \(\vec{P}+\vec{Q}-\vec{R}=0\) angle between \(\vec{P}\) and \(\vec{Q}\) is \(\theta_{1}\). If \(\vec{P}+\vec{Q}-\vec{S}=0\) angle between \(\vec{P}\) and \(\vec{S}\) is \(\theta_{2}\). The ratio of \(\theta_{1}\) to \(\theta_{2}\) is

269905 Two light strings of length\(4 \mathrm{~cm}\) and \(3 \mathrm{~cm}\) are tied to a bob of weight \(500 \mathrm{gm}\). The free ends of the strings are tied to pegs in the same horizontal line and separated by \(5 \mathrm{~cm}\).The ratio of tension in the longer string to that in the shorter string is

269939 The greatest and least resultant of two forces acting at a point are \(29 \mathrm{Kg} \mathrm{wt}\). and \(5 \mathrm{Kg} \mathrm{wt}\). respectively. If each force is increased by 3 \(\mathrm{Kg}\) wt. the magnitude of the resultant of new forces acting at right angles to each other is

269940 Two forces \(\mathbf{P}\) and \(\mathbf{Q}\) act at an angle of \(120^{\circ}\) with each other. If the resultant is at right angles to \(P\) and \(P\) is equal to \(4 \mathrm{~kg}\)-wt, then the value of \(Q\) is

269941 The resultant of two vectors \(\vec{P} \& \vec{Q}\) is \(\vec{R}\). If the magnitude of \(\vec{Q}\) is doubled the new resultant becomes perpendicular to \(\overrightarrow{\mathrm{p}}\) then magnitude of \(\vec{R}\) is

269942 \(\quad \vec{P}, \vec{Q}, \vec{R}, \vec{S}\) are vector of equal magnitude. If \(\vec{P}+\vec{Q}-\vec{R}=0\) angle between \(\vec{P}\) and \(\vec{Q}\) is \(\theta_{1}\). If \(\vec{P}+\vec{Q}-\vec{S}=0\) angle between \(\vec{P}\) and \(\vec{S}\) is \(\theta_{2}\). The ratio of \(\theta_{1}\) to \(\theta_{2}\) is

269905 Two light strings of length\(4 \mathrm{~cm}\) and \(3 \mathrm{~cm}\) are tied to a bob of weight \(500 \mathrm{gm}\). The free ends of the strings are tied to pegs in the same horizontal line and separated by \(5 \mathrm{~cm}\).The ratio of tension in the longer string to that in the shorter string is

269939 The greatest and least resultant of two forces acting at a point are \(29 \mathrm{Kg} \mathrm{wt}\). and \(5 \mathrm{Kg} \mathrm{wt}\). respectively. If each force is increased by 3 \(\mathrm{Kg}\) wt. the magnitude of the resultant of new forces acting at right angles to each other is

269940 Two forces \(\mathbf{P}\) and \(\mathbf{Q}\) act at an angle of \(120^{\circ}\) with each other. If the resultant is at right angles to \(P\) and \(P\) is equal to \(4 \mathrm{~kg}\)-wt, then the value of \(Q\) is

269941 The resultant of two vectors \(\vec{P} \& \vec{Q}\) is \(\vec{R}\). If the magnitude of \(\vec{Q}\) is doubled the new resultant becomes perpendicular to \(\overrightarrow{\mathrm{p}}\) then magnitude of \(\vec{R}\) is

269942 \(\quad \vec{P}, \vec{Q}, \vec{R}, \vec{S}\) are vector of equal magnitude. If \(\vec{P}+\vec{Q}-\vec{R}=0\) angle between \(\vec{P}\) and \(\vec{Q}\) is \(\theta_{1}\). If \(\vec{P}+\vec{Q}-\vec{S}=0\) angle between \(\vec{P}\) and \(\vec{S}\) is \(\theta_{2}\). The ratio of \(\theta_{1}\) to \(\theta_{2}\) is