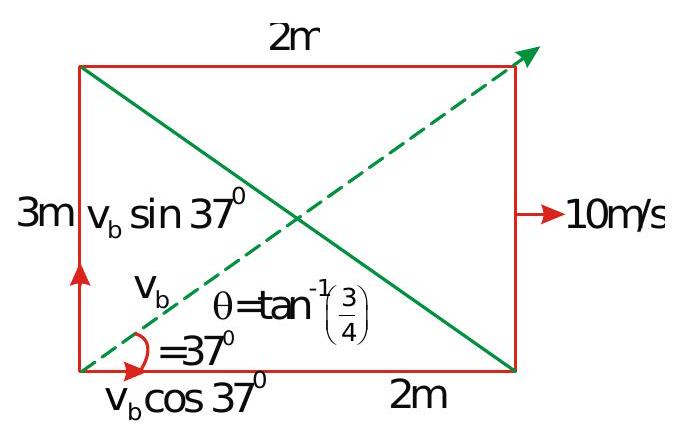
269816 An armored car \(2 \mathrm{~m}\) long and \(3 \mathrm{~m}\) wide is moving at \(10 \mathrm{~ms}^{-1}\) when a bullet hits it in a direction making an angle \(\tan ^{-1}\left(\frac{3}{4}\right)\) with the length of the car as seen by a stationary observer. The bullet enters one edge of the car at the corner and passes out at the diagonally opposite corner. Neglecting any interaction between the car and thebullet and effect of gravity, the time for the bullet to cross the car is
269817 Two particles start simultaneously from the same point andmovealong two straight lines. One with uniform velocity v and other with a uniform acceleration a. If \(\alpha\) is the angle between the lines of motion of two particlesthen the least value of relative velocity will be at time given by
269816 An armored car \(2 \mathrm{~m}\) long and \(3 \mathrm{~m}\) wide is moving at \(10 \mathrm{~ms}^{-1}\) when a bullet hits it in a direction making an angle \(\tan ^{-1}\left(\frac{3}{4}\right)\) with the length of the car as seen by a stationary observer. The bullet enters one edge of the car at the corner and passes out at the diagonally opposite corner. Neglecting any interaction between the car and thebullet and effect of gravity, the time for the bullet to cross the car is
269817 Two particles start simultaneously from the same point andmovealong two straight lines. One with uniform velocity v and other with a uniform acceleration a. If \(\alpha\) is the angle between the lines of motion of two particlesthen the least value of relative velocity will be at time given by
269816 An armored car \(2 \mathrm{~m}\) long and \(3 \mathrm{~m}\) wide is moving at \(10 \mathrm{~ms}^{-1}\) when a bullet hits it in a direction making an angle \(\tan ^{-1}\left(\frac{3}{4}\right)\) with the length of the car as seen by a stationary observer. The bullet enters one edge of the car at the corner and passes out at the diagonally opposite corner. Neglecting any interaction between the car and thebullet and effect of gravity, the time for the bullet to cross the car is
269817 Two particles start simultaneously from the same point andmovealong two straight lines. One with uniform velocity v and other with a uniform acceleration a. If \(\alpha\) is the angle between the lines of motion of two particlesthen the least value of relative velocity will be at time given by