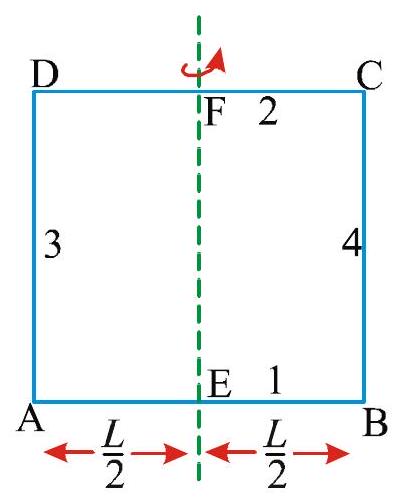
269627 Two rings of the same radius \(R\) and mass \(M\) are placed such that their centres coincide and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the common centre and perpendicular to the plane of one of the rings is

269628 In the above problem, the moment of inertia of the system about an axis passing through the diameters of both rings is

269629 Four thin metal rods, each of mass \(M\) and length \(L\), are welded to form a square \(A B C D\) as shown in figure. The moment of inertia of the composite structure about a line which bisects rods \(A B\) and \(C D\) is

269630 Two circular loops \(A\) and \(B\) are made of the same wire and their radii are in the ratio \(1: n\).
Their moments of inertia about the axis passing through the centre and perpendicular to their planes are in the ratio \(1: \mathrm{m}\). The relation between \(m\) and \(n\) is

269627 Two rings of the same radius \(R\) and mass \(M\) are placed such that their centres coincide and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the common centre and perpendicular to the plane of one of the rings is

269628 In the above problem, the moment of inertia of the system about an axis passing through the diameters of both rings is

269629 Four thin metal rods, each of mass \(M\) and length \(L\), are welded to form a square \(A B C D\) as shown in figure. The moment of inertia of the composite structure about a line which bisects rods \(A B\) and \(C D\) is

269630 Two circular loops \(A\) and \(B\) are made of the same wire and their radii are in the ratio \(1: n\).
Their moments of inertia about the axis passing through the centre and perpendicular to their planes are in the ratio \(1: \mathrm{m}\). The relation between \(m\) and \(n\) is

269627 Two rings of the same radius \(R\) and mass \(M\) are placed such that their centres coincide and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the common centre and perpendicular to the plane of one of the rings is

269628 In the above problem, the moment of inertia of the system about an axis passing through the diameters of both rings is

269629 Four thin metal rods, each of mass \(M\) and length \(L\), are welded to form a square \(A B C D\) as shown in figure. The moment of inertia of the composite structure about a line which bisects rods \(A B\) and \(C D\) is

269630 Two circular loops \(A\) and \(B\) are made of the same wire and their radii are in the ratio \(1: n\).
Their moments of inertia about the axis passing through the centre and perpendicular to their planes are in the ratio \(1: \mathrm{m}\). The relation between \(m\) and \(n\) is

269627 Two rings of the same radius \(R\) and mass \(M\) are placed such that their centres coincide and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the common centre and perpendicular to the plane of one of the rings is

269628 In the above problem, the moment of inertia of the system about an axis passing through the diameters of both rings is

269629 Four thin metal rods, each of mass \(M\) and length \(L\), are welded to form a square \(A B C D\) as shown in figure. The moment of inertia of the composite structure about a line which bisects rods \(A B\) and \(C D\) is

269630 Two circular loops \(A\) and \(B\) are made of the same wire and their radii are in the ratio \(1: n\).
Their moments of inertia about the axis passing through the centre and perpendicular to their planes are in the ratio \(1: \mathrm{m}\). The relation between \(m\) and \(n\) is