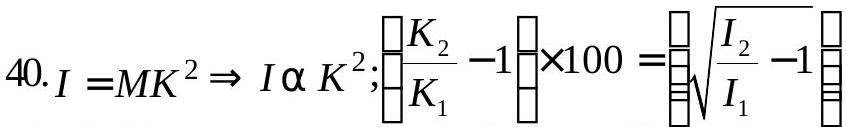269397 The radius of gyration of a body is\(18 \mathrm{~cm}\) when it is rotating about an axis passing through centre of mass of body. If radius of gyration of same body is \(30 \mathrm{~cm}\) about a parallel axis to first axis then, perpendicular distance between two parallel axes is
269397 The radius of gyration of a body is\(18 \mathrm{~cm}\) when it is rotating about an axis passing through centre of mass of body. If radius of gyration of same body is \(30 \mathrm{~cm}\) about a parallel axis to first axis then, perpendicular distance between two parallel axes is
269397 The radius of gyration of a body is\(18 \mathrm{~cm}\) when it is rotating about an axis passing through centre of mass of body. If radius of gyration of same body is \(30 \mathrm{~cm}\) about a parallel axis to first axis then, perpendicular distance between two parallel axes is
269397 The radius of gyration of a body is\(18 \mathrm{~cm}\) when it is rotating about an axis passing through centre of mass of body. If radius of gyration of same body is \(30 \mathrm{~cm}\) about a parallel axis to first axis then, perpendicular distance between two parallel axes is