268880 A lifting machine, having an efficiency of \(\mathbf{8 0 \%}\) uses \(2500 \mathrm{~J}\) of energy in lifting a \(10 \mathrm{~kg}\) load over a certain height. If the load is now allowed to fall through that height freely, its velocity at the end of the fall will be ( \(g=10 \mathrm{~m} / \mathrm{s}^{2}\) )

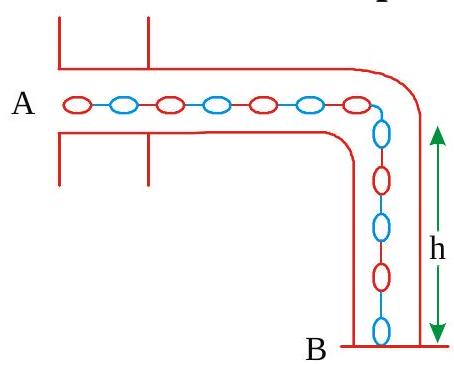
268881 A chain \(A B\) of length \(L\) is lying in a smooth horizontal tube so that a fraction \(h\) of its length L, hangs freely and touches the surface of the table with its end B. At a certain moment, the end \(A\) of the chain is set free. The velocity of end A of the chain, when it slips out of tube, is

268882 A block of mass \(m=1 \mathrm{~kg}\) moving on a horizontal surface with speed \(v_{i}=2 \mathrm{~ms}^{-1}\) enters a rough patch ranging from \(x=0.10 \mathrm{~m}\) to \(x=2.01 \mathrm{~m}\). The retarding force \(F_{r}=\frac{-k}{x}\) for \(0.1 \mathrm{~m}

268883 A \(1.5 \mathrm{~kg}\) block is initially at rest on a horizontal frictionless surface. A horizontal force \(\vec{F}=\left(4-x^{2}\right) \hat{i}\) is applied on the block . Initial position of the block is at \(x=0\). The maximum kinetic energy of the block between \(x=0\) and \(x=2 m\) is

268880 A lifting machine, having an efficiency of \(\mathbf{8 0 \%}\) uses \(2500 \mathrm{~J}\) of energy in lifting a \(10 \mathrm{~kg}\) load over a certain height. If the load is now allowed to fall through that height freely, its velocity at the end of the fall will be ( \(g=10 \mathrm{~m} / \mathrm{s}^{2}\) )

268881 A chain \(A B\) of length \(L\) is lying in a smooth horizontal tube so that a fraction \(h\) of its length L, hangs freely and touches the surface of the table with its end B. At a certain moment, the end \(A\) of the chain is set free. The velocity of end A of the chain, when it slips out of tube, is

268882 A block of mass \(m=1 \mathrm{~kg}\) moving on a horizontal surface with speed \(v_{i}=2 \mathrm{~ms}^{-1}\) enters a rough patch ranging from \(x=0.10 \mathrm{~m}\) to \(x=2.01 \mathrm{~m}\). The retarding force \(F_{r}=\frac{-k}{x}\) for \(0.1 \mathrm{~m}

268883 A \(1.5 \mathrm{~kg}\) block is initially at rest on a horizontal frictionless surface. A horizontal force \(\vec{F}=\left(4-x^{2}\right) \hat{i}\) is applied on the block . Initial position of the block is at \(x=0\). The maximum kinetic energy of the block between \(x=0\) and \(x=2 m\) is

268880 A lifting machine, having an efficiency of \(\mathbf{8 0 \%}\) uses \(2500 \mathrm{~J}\) of energy in lifting a \(10 \mathrm{~kg}\) load over a certain height. If the load is now allowed to fall through that height freely, its velocity at the end of the fall will be ( \(g=10 \mathrm{~m} / \mathrm{s}^{2}\) )

268881 A chain \(A B\) of length \(L\) is lying in a smooth horizontal tube so that a fraction \(h\) of its length L, hangs freely and touches the surface of the table with its end B. At a certain moment, the end \(A\) of the chain is set free. The velocity of end A of the chain, when it slips out of tube, is

268882 A block of mass \(m=1 \mathrm{~kg}\) moving on a horizontal surface with speed \(v_{i}=2 \mathrm{~ms}^{-1}\) enters a rough patch ranging from \(x=0.10 \mathrm{~m}\) to \(x=2.01 \mathrm{~m}\). The retarding force \(F_{r}=\frac{-k}{x}\) for \(0.1 \mathrm{~m}

268883 A \(1.5 \mathrm{~kg}\) block is initially at rest on a horizontal frictionless surface. A horizontal force \(\vec{F}=\left(4-x^{2}\right) \hat{i}\) is applied on the block . Initial position of the block is at \(x=0\). The maximum kinetic energy of the block between \(x=0\) and \(x=2 m\) is

268880 A lifting machine, having an efficiency of \(\mathbf{8 0 \%}\) uses \(2500 \mathrm{~J}\) of energy in lifting a \(10 \mathrm{~kg}\) load over a certain height. If the load is now allowed to fall through that height freely, its velocity at the end of the fall will be ( \(g=10 \mathrm{~m} / \mathrm{s}^{2}\) )

268881 A chain \(A B\) of length \(L\) is lying in a smooth horizontal tube so that a fraction \(h\) of its length L, hangs freely and touches the surface of the table with its end B. At a certain moment, the end \(A\) of the chain is set free. The velocity of end A of the chain, when it slips out of tube, is

268882 A block of mass \(m=1 \mathrm{~kg}\) moving on a horizontal surface with speed \(v_{i}=2 \mathrm{~ms}^{-1}\) enters a rough patch ranging from \(x=0.10 \mathrm{~m}\) to \(x=2.01 \mathrm{~m}\). The retarding force \(F_{r}=\frac{-k}{x}\) for \(0.1 \mathrm{~m}

268883 A \(1.5 \mathrm{~kg}\) block is initially at rest on a horizontal frictionless surface. A horizontal force \(\vec{F}=\left(4-x^{2}\right) \hat{i}\) is applied on the block . Initial position of the block is at \(x=0\). The maximum kinetic energy of the block between \(x=0\) and \(x=2 m\) is