268871
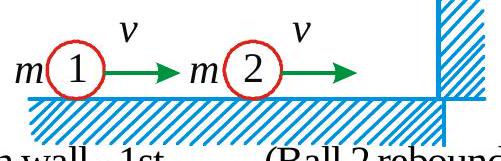
Two balls each of mass '\(m\) ' are moving with same velocity \(v\) on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is \(\quad(2008 \mathrm{M})\)
268871
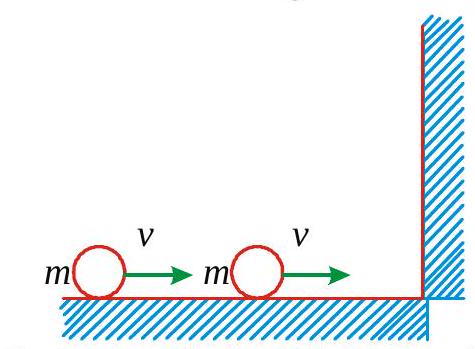
Two balls each of mass '\(m\) ' are moving with same velocity \(v\) on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is \(\quad(2008 \mathrm{M})\)