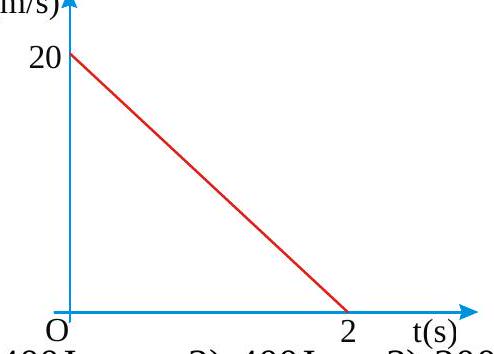
268842 An object of mass\(5 \mathrm{~kg}\) falls from rest through a vertical distance of \(20 \mathrm{~m}\) and attains a velocity of \(10 \mathrm{~m} / \mathrm{s}\). How much work is done by the resistance of the air on the object \(\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)

268843 The velocity of a \(2 \mathbf{k g}\) body is changed from \((4 \hat{i}+3 \hat{j}) \mathbf{~ m s}^{-1}\) to \(6 \mathbf{~ m s}^{-1}\). The work done on the body is

268844 Anout fielder throws a cricket ball with an initial kinetic energy of \(800 \mathrm{~J}\) and an infielder catches the ball when its kinetic energy is \(600 \mathrm{~J}\). If the path of the ball between them is assumed straight and is \(20 \mathrm{~m}\) long, the air resistance acting on the ball is

268845 Velocity -time graph of a particle of mass\(2 \mathrm{~kg}\) moving in a straight line is as shown in the figure. Work done by all the forces on the particle is \(\mathrm{V}(\mathrm{m} / \mathrm{s})^{4}\)

268846 A block of mass of\(1 \mathrm{~kg}\) slides down a curved track that is one -quadrant of circle of radius \(1 \mathrm{~m}\). Its speed at the bottom is \(2 \mathrm{~m} / \mathrm{s}\). The workdone by the frictional force is

268842 An object of mass\(5 \mathrm{~kg}\) falls from rest through a vertical distance of \(20 \mathrm{~m}\) and attains a velocity of \(10 \mathrm{~m} / \mathrm{s}\). How much work is done by the resistance of the air on the object \(\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)

268843 The velocity of a \(2 \mathbf{k g}\) body is changed from \((4 \hat{i}+3 \hat{j}) \mathbf{~ m s}^{-1}\) to \(6 \mathbf{~ m s}^{-1}\). The work done on the body is

268844 Anout fielder throws a cricket ball with an initial kinetic energy of \(800 \mathrm{~J}\) and an infielder catches the ball when its kinetic energy is \(600 \mathrm{~J}\). If the path of the ball between them is assumed straight and is \(20 \mathrm{~m}\) long, the air resistance acting on the ball is

268845 Velocity -time graph of a particle of mass\(2 \mathrm{~kg}\) moving in a straight line is as shown in the figure. Work done by all the forces on the particle is \(\mathrm{V}(\mathrm{m} / \mathrm{s})^{4}\)

268846 A block of mass of\(1 \mathrm{~kg}\) slides down a curved track that is one -quadrant of circle of radius \(1 \mathrm{~m}\). Its speed at the bottom is \(2 \mathrm{~m} / \mathrm{s}\). The workdone by the frictional force is

268842 An object of mass\(5 \mathrm{~kg}\) falls from rest through a vertical distance of \(20 \mathrm{~m}\) and attains a velocity of \(10 \mathrm{~m} / \mathrm{s}\). How much work is done by the resistance of the air on the object \(\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)

268843 The velocity of a \(2 \mathbf{k g}\) body is changed from \((4 \hat{i}+3 \hat{j}) \mathbf{~ m s}^{-1}\) to \(6 \mathbf{~ m s}^{-1}\). The work done on the body is

268844 Anout fielder throws a cricket ball with an initial kinetic energy of \(800 \mathrm{~J}\) and an infielder catches the ball when its kinetic energy is \(600 \mathrm{~J}\). If the path of the ball between them is assumed straight and is \(20 \mathrm{~m}\) long, the air resistance acting on the ball is

268845 Velocity -time graph of a particle of mass\(2 \mathrm{~kg}\) moving in a straight line is as shown in the figure. Work done by all the forces on the particle is \(\mathrm{V}(\mathrm{m} / \mathrm{s})^{4}\)

268846 A block of mass of\(1 \mathrm{~kg}\) slides down a curved track that is one -quadrant of circle of radius \(1 \mathrm{~m}\). Its speed at the bottom is \(2 \mathrm{~m} / \mathrm{s}\). The workdone by the frictional force is

268842 An object of mass\(5 \mathrm{~kg}\) falls from rest through a vertical distance of \(20 \mathrm{~m}\) and attains a velocity of \(10 \mathrm{~m} / \mathrm{s}\). How much work is done by the resistance of the air on the object \(\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)

268843 The velocity of a \(2 \mathbf{k g}\) body is changed from \((4 \hat{i}+3 \hat{j}) \mathbf{~ m s}^{-1}\) to \(6 \mathbf{~ m s}^{-1}\). The work done on the body is

268844 Anout fielder throws a cricket ball with an initial kinetic energy of \(800 \mathrm{~J}\) and an infielder catches the ball when its kinetic energy is \(600 \mathrm{~J}\). If the path of the ball between them is assumed straight and is \(20 \mathrm{~m}\) long, the air resistance acting on the ball is

268845 Velocity -time graph of a particle of mass\(2 \mathrm{~kg}\) moving in a straight line is as shown in the figure. Work done by all the forces on the particle is \(\mathrm{V}(\mathrm{m} / \mathrm{s})^{4}\)

268846 A block of mass of\(1 \mathrm{~kg}\) slides down a curved track that is one -quadrant of circle of radius \(1 \mathrm{~m}\). Its speed at the bottom is \(2 \mathrm{~m} / \mathrm{s}\). The workdone by the frictional force is

268842 An object of mass\(5 \mathrm{~kg}\) falls from rest through a vertical distance of \(20 \mathrm{~m}\) and attains a velocity of \(10 \mathrm{~m} / \mathrm{s}\). How much work is done by the resistance of the air on the object \(\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)

268843 The velocity of a \(2 \mathbf{k g}\) body is changed from \((4 \hat{i}+3 \hat{j}) \mathbf{~ m s}^{-1}\) to \(6 \mathbf{~ m s}^{-1}\). The work done on the body is

268844 Anout fielder throws a cricket ball with an initial kinetic energy of \(800 \mathrm{~J}\) and an infielder catches the ball when its kinetic energy is \(600 \mathrm{~J}\). If the path of the ball between them is assumed straight and is \(20 \mathrm{~m}\) long, the air resistance acting on the ball is

268845 Velocity -time graph of a particle of mass\(2 \mathrm{~kg}\) moving in a straight line is as shown in the figure. Work done by all the forces on the particle is \(\mathrm{V}(\mathrm{m} / \mathrm{s})^{4}\)

268846 A block of mass of\(1 \mathrm{~kg}\) slides down a curved track that is one -quadrant of circle of radius \(1 \mathrm{~m}\). Its speed at the bottom is \(2 \mathrm{~m} / \mathrm{s}\). The workdone by the frictional force is