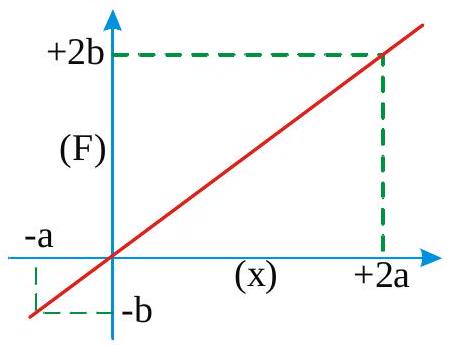
268753 A block of mass\(5 \mathrm{~kg}\) initially at rest at the origin is acted upon by a force along the positive \(X\) - direction represented by \(F=(20+5 x) N\). Calculate the work done by the force during the displacement of the block from \(x=0\) to \(x=4 \mathrm{~m}\).

268754 A force\(F\) acting on a particle varies with the position \(x\) as shown in the graph. Find the work done by the force in displacing the particle from \(x=-\) a to \(x=+2 \mathrm{a}\)

268755 A force\(\vec{F}=(2 \hat{i}+3 \hat{j}-4 \hat{k}) N\) acts on a particle which is constrained to move in the XOY plane along the line \(\mathbf{x}=\mathbf{y}\). If the particle moves \(5 \sqrt{2} \mathrm{~m}\), the work done by force in joule is

268756 Two forces each of magnitude\(10 \mathrm{~N}\) act simultaneously on a body with their directions inclined to each other at an angle of \(120^{\circ}\) and displaces the body over \(10 \mathrm{~m}\) along the bisector of the angle between the two forces. Then the work done by each force is

268753 A block of mass\(5 \mathrm{~kg}\) initially at rest at the origin is acted upon by a force along the positive \(X\) - direction represented by \(F=(20+5 x) N\). Calculate the work done by the force during the displacement of the block from \(x=0\) to \(x=4 \mathrm{~m}\).

268754 A force\(F\) acting on a particle varies with the position \(x\) as shown in the graph. Find the work done by the force in displacing the particle from \(x=-\) a to \(x=+2 \mathrm{a}\)

268755 A force\(\vec{F}=(2 \hat{i}+3 \hat{j}-4 \hat{k}) N\) acts on a particle which is constrained to move in the XOY plane along the line \(\mathbf{x}=\mathbf{y}\). If the particle moves \(5 \sqrt{2} \mathrm{~m}\), the work done by force in joule is

268756 Two forces each of magnitude\(10 \mathrm{~N}\) act simultaneously on a body with their directions inclined to each other at an angle of \(120^{\circ}\) and displaces the body over \(10 \mathrm{~m}\) along the bisector of the angle between the two forces. Then the work done by each force is

268753 A block of mass\(5 \mathrm{~kg}\) initially at rest at the origin is acted upon by a force along the positive \(X\) - direction represented by \(F=(20+5 x) N\). Calculate the work done by the force during the displacement of the block from \(x=0\) to \(x=4 \mathrm{~m}\).

268754 A force\(F\) acting on a particle varies with the position \(x\) as shown in the graph. Find the work done by the force in displacing the particle from \(x=-\) a to \(x=+2 \mathrm{a}\)

268755 A force\(\vec{F}=(2 \hat{i}+3 \hat{j}-4 \hat{k}) N\) acts on a particle which is constrained to move in the XOY plane along the line \(\mathbf{x}=\mathbf{y}\). If the particle moves \(5 \sqrt{2} \mathrm{~m}\), the work done by force in joule is

268756 Two forces each of magnitude\(10 \mathrm{~N}\) act simultaneously on a body with their directions inclined to each other at an angle of \(120^{\circ}\) and displaces the body over \(10 \mathrm{~m}\) along the bisector of the angle between the two forces. Then the work done by each force is

268753 A block of mass\(5 \mathrm{~kg}\) initially at rest at the origin is acted upon by a force along the positive \(X\) - direction represented by \(F=(20+5 x) N\). Calculate the work done by the force during the displacement of the block from \(x=0\) to \(x=4 \mathrm{~m}\).

268754 A force\(F\) acting on a particle varies with the position \(x\) as shown in the graph. Find the work done by the force in displacing the particle from \(x=-\) a to \(x=+2 \mathrm{a}\)

268755 A force\(\vec{F}=(2 \hat{i}+3 \hat{j}-4 \hat{k}) N\) acts on a particle which is constrained to move in the XOY plane along the line \(\mathbf{x}=\mathbf{y}\). If the particle moves \(5 \sqrt{2} \mathrm{~m}\), the work done by force in joule is

268756 Two forces each of magnitude\(10 \mathrm{~N}\) act simultaneously on a body with their directions inclined to each other at an angle of \(120^{\circ}\) and displaces the body over \(10 \mathrm{~m}\) along the bisector of the angle between the two forces. Then the work done by each force is