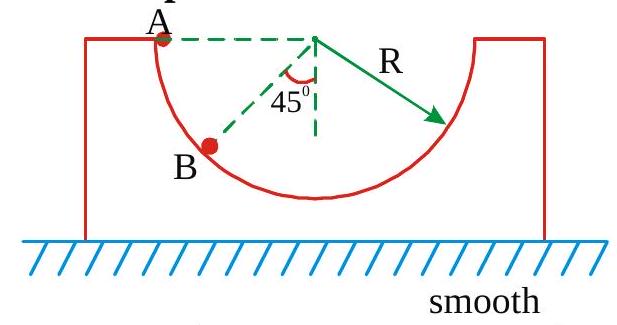
268886 The potential energy of a particle of mass \(m\) is given by \(U=\frac{1}{2} k x^{2}\) for \(\mathbf{x}<\mathbf{0}\) and \(\mathbf{U}=\mathbf{0}\) for \(x \geq 0\). If total mechanical energy of the particle is \(\mathbf{E}\). Then its speed at \(x=\sqrt{\frac{2 E}{k}}\) is

268887 A \(1 \mathrm{~kg}\) block situated on a rough inclined plane is connected to spring of a spring constant \(100 \mathrm{Nm}^{-1}\) as shown in fig. The block is released from rest with the spring in the unstretched position. The block moves \(10 \mathrm{~cm}\) down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.
\(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
1

268888 A light spring of force constant ' \(K\) ' is held between two blocks of masses ' \(m\) ' and ' \(2 \mathrm{~m}\) '. The two blocks and the spring system rests on a smooth horizontal floor. Now the blocks are moved towards each other compressing the spring by ' \(x\) ' and suddenly released. The relative velocity between the blocks when the spring attains its natural length will be

268889 A ball of mass \(m\) is released from \(A\) inside a smooth wedge of mass \(m\) as shown in fig. What is the speed of the wedge when the ball reaches point \(B\) ?

268886 The potential energy of a particle of mass \(m\) is given by \(U=\frac{1}{2} k x^{2}\) for \(\mathbf{x}<\mathbf{0}\) and \(\mathbf{U}=\mathbf{0}\) for \(x \geq 0\). If total mechanical energy of the particle is \(\mathbf{E}\). Then its speed at \(x=\sqrt{\frac{2 E}{k}}\) is

268887 A \(1 \mathrm{~kg}\) block situated on a rough inclined plane is connected to spring of a spring constant \(100 \mathrm{Nm}^{-1}\) as shown in fig. The block is released from rest with the spring in the unstretched position. The block moves \(10 \mathrm{~cm}\) down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.
\(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
1

268888 A light spring of force constant ' \(K\) ' is held between two blocks of masses ' \(m\) ' and ' \(2 \mathrm{~m}\) '. The two blocks and the spring system rests on a smooth horizontal floor. Now the blocks are moved towards each other compressing the spring by ' \(x\) ' and suddenly released. The relative velocity between the blocks when the spring attains its natural length will be

268889 A ball of mass \(m\) is released from \(A\) inside a smooth wedge of mass \(m\) as shown in fig. What is the speed of the wedge when the ball reaches point \(B\) ?

268886 The potential energy of a particle of mass \(m\) is given by \(U=\frac{1}{2} k x^{2}\) for \(\mathbf{x}<\mathbf{0}\) and \(\mathbf{U}=\mathbf{0}\) for \(x \geq 0\). If total mechanical energy of the particle is \(\mathbf{E}\). Then its speed at \(x=\sqrt{\frac{2 E}{k}}\) is

268887 A \(1 \mathrm{~kg}\) block situated on a rough inclined plane is connected to spring of a spring constant \(100 \mathrm{Nm}^{-1}\) as shown in fig. The block is released from rest with the spring in the unstretched position. The block moves \(10 \mathrm{~cm}\) down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.
\(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
1

268888 A light spring of force constant ' \(K\) ' is held between two blocks of masses ' \(m\) ' and ' \(2 \mathrm{~m}\) '. The two blocks and the spring system rests on a smooth horizontal floor. Now the blocks are moved towards each other compressing the spring by ' \(x\) ' and suddenly released. The relative velocity between the blocks when the spring attains its natural length will be

268889 A ball of mass \(m\) is released from \(A\) inside a smooth wedge of mass \(m\) as shown in fig. What is the speed of the wedge when the ball reaches point \(B\) ?

268886 The potential energy of a particle of mass \(m\) is given by \(U=\frac{1}{2} k x^{2}\) for \(\mathbf{x}<\mathbf{0}\) and \(\mathbf{U}=\mathbf{0}\) for \(x \geq 0\). If total mechanical energy of the particle is \(\mathbf{E}\). Then its speed at \(x=\sqrt{\frac{2 E}{k}}\) is

268887 A \(1 \mathrm{~kg}\) block situated on a rough inclined plane is connected to spring of a spring constant \(100 \mathrm{Nm}^{-1}\) as shown in fig. The block is released from rest with the spring in the unstretched position. The block moves \(10 \mathrm{~cm}\) down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.
\(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
1

268888 A light spring of force constant ' \(K\) ' is held between two blocks of masses ' \(m\) ' and ' \(2 \mathrm{~m}\) '. The two blocks and the spring system rests on a smooth horizontal floor. Now the blocks are moved towards each other compressing the spring by ' \(x\) ' and suddenly released. The relative velocity between the blocks when the spring attains its natural length will be

268889 A ball of mass \(m\) is released from \(A\) inside a smooth wedge of mass \(m\) as shown in fig. What is the speed of the wedge when the ball reaches point \(B\) ?