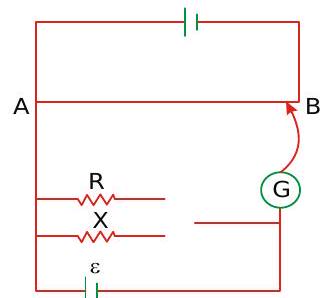
268465 In the determination of the internal resistance of a cell using a potentiometer, when the cell is shunted by a resistance " \(R\) " and connected in the secondary circuit, the balance length is found to be \(L_{1}\). O n doubling the shunt resistance, the balance length is found to increase to \(L_{2^{\prime}}\) The value of the internal resistance is

268466 Figure shows a potentiometer circuit for comparision of two resistances. The balance point with a standard resistor \(R=10.0 \Omega\) is found to be \(58.3 \mathrm{~cm}\), while that with the unknown resistance \(X\) is \(68.5 \mathrm{~cm}\). T he value of \(X\) is

268467 In a experiment for calibration of voltmeter a standard cell of emf \(1.5 \mathrm{~V}\) is balanced at \(300 \mathrm{~cm}\) length of potentiometer wire. The P.D across a resistance in the circuit is balancedat \(1.25 \mathrm{~m}\). If a voltmeter is connected across the same resistance it reads \(0.65 \mathrm{~V}\). The error in the volt meter is

268468 The current in the primay circuit of a potentiometer is \(0.2 \mathrm{~A}\). T he specific resistance and cross-section of the potentiometer wire are \(4 \times 10^{-7} \mathrm{~m}^{2}\), respectively. The potential gradient will be equal to [M ains-2011]

268510 A potentiometer wire\(10 \mathrm{~m}\) long has a resistance of \(40 \Omega\). It is connected in series with a resistanced box and a \(2 \mathrm{v}\) storage cell. If the potential gradient along the wire is \(0.01 \mathrm{~V} / \mathrm{m}\) the resistance unplugged in the box is

268465 In the determination of the internal resistance of a cell using a potentiometer, when the cell is shunted by a resistance " \(R\) " and connected in the secondary circuit, the balance length is found to be \(L_{1}\). O n doubling the shunt resistance, the balance length is found to increase to \(L_{2^{\prime}}\) The value of the internal resistance is

268466 Figure shows a potentiometer circuit for comparision of two resistances. The balance point with a standard resistor \(R=10.0 \Omega\) is found to be \(58.3 \mathrm{~cm}\), while that with the unknown resistance \(X\) is \(68.5 \mathrm{~cm}\). T he value of \(X\) is

268467 In a experiment for calibration of voltmeter a standard cell of emf \(1.5 \mathrm{~V}\) is balanced at \(300 \mathrm{~cm}\) length of potentiometer wire. The P.D across a resistance in the circuit is balancedat \(1.25 \mathrm{~m}\). If a voltmeter is connected across the same resistance it reads \(0.65 \mathrm{~V}\). The error in the volt meter is

268468 The current in the primay circuit of a potentiometer is \(0.2 \mathrm{~A}\). T he specific resistance and cross-section of the potentiometer wire are \(4 \times 10^{-7} \mathrm{~m}^{2}\), respectively. The potential gradient will be equal to [M ains-2011]

268510 A potentiometer wire\(10 \mathrm{~m}\) long has a resistance of \(40 \Omega\). It is connected in series with a resistanced box and a \(2 \mathrm{v}\) storage cell. If the potential gradient along the wire is \(0.01 \mathrm{~V} / \mathrm{m}\) the resistance unplugged in the box is

268465 In the determination of the internal resistance of a cell using a potentiometer, when the cell is shunted by a resistance " \(R\) " and connected in the secondary circuit, the balance length is found to be \(L_{1}\). O n doubling the shunt resistance, the balance length is found to increase to \(L_{2^{\prime}}\) The value of the internal resistance is

268466 Figure shows a potentiometer circuit for comparision of two resistances. The balance point with a standard resistor \(R=10.0 \Omega\) is found to be \(58.3 \mathrm{~cm}\), while that with the unknown resistance \(X\) is \(68.5 \mathrm{~cm}\). T he value of \(X\) is

268467 In a experiment for calibration of voltmeter a standard cell of emf \(1.5 \mathrm{~V}\) is balanced at \(300 \mathrm{~cm}\) length of potentiometer wire. The P.D across a resistance in the circuit is balancedat \(1.25 \mathrm{~m}\). If a voltmeter is connected across the same resistance it reads \(0.65 \mathrm{~V}\). The error in the volt meter is

268468 The current in the primay circuit of a potentiometer is \(0.2 \mathrm{~A}\). T he specific resistance and cross-section of the potentiometer wire are \(4 \times 10^{-7} \mathrm{~m}^{2}\), respectively. The potential gradient will be equal to [M ains-2011]

268510 A potentiometer wire\(10 \mathrm{~m}\) long has a resistance of \(40 \Omega\). It is connected in series with a resistanced box and a \(2 \mathrm{v}\) storage cell. If the potential gradient along the wire is \(0.01 \mathrm{~V} / \mathrm{m}\) the resistance unplugged in the box is

268465 In the determination of the internal resistance of a cell using a potentiometer, when the cell is shunted by a resistance " \(R\) " and connected in the secondary circuit, the balance length is found to be \(L_{1}\). O n doubling the shunt resistance, the balance length is found to increase to \(L_{2^{\prime}}\) The value of the internal resistance is

268466 Figure shows a potentiometer circuit for comparision of two resistances. The balance point with a standard resistor \(R=10.0 \Omega\) is found to be \(58.3 \mathrm{~cm}\), while that with the unknown resistance \(X\) is \(68.5 \mathrm{~cm}\). T he value of \(X\) is

268467 In a experiment for calibration of voltmeter a standard cell of emf \(1.5 \mathrm{~V}\) is balanced at \(300 \mathrm{~cm}\) length of potentiometer wire. The P.D across a resistance in the circuit is balancedat \(1.25 \mathrm{~m}\). If a voltmeter is connected across the same resistance it reads \(0.65 \mathrm{~V}\). The error in the volt meter is

268468 The current in the primay circuit of a potentiometer is \(0.2 \mathrm{~A}\). T he specific resistance and cross-section of the potentiometer wire are \(4 \times 10^{-7} \mathrm{~m}^{2}\), respectively. The potential gradient will be equal to [M ains-2011]

268510 A potentiometer wire\(10 \mathrm{~m}\) long has a resistance of \(40 \Omega\). It is connected in series with a resistanced box and a \(2 \mathrm{v}\) storage cell. If the potential gradient along the wire is \(0.01 \mathrm{~V} / \mathrm{m}\) the resistance unplugged in the box is

268465 In the determination of the internal resistance of a cell using a potentiometer, when the cell is shunted by a resistance " \(R\) " and connected in the secondary circuit, the balance length is found to be \(L_{1}\). O n doubling the shunt resistance, the balance length is found to increase to \(L_{2^{\prime}}\) The value of the internal resistance is

268466 Figure shows a potentiometer circuit for comparision of two resistances. The balance point with a standard resistor \(R=10.0 \Omega\) is found to be \(58.3 \mathrm{~cm}\), while that with the unknown resistance \(X\) is \(68.5 \mathrm{~cm}\). T he value of \(X\) is

268467 In a experiment for calibration of voltmeter a standard cell of emf \(1.5 \mathrm{~V}\) is balanced at \(300 \mathrm{~cm}\) length of potentiometer wire. The P.D across a resistance in the circuit is balancedat \(1.25 \mathrm{~m}\). If a voltmeter is connected across the same resistance it reads \(0.65 \mathrm{~V}\). The error in the volt meter is

268468 The current in the primay circuit of a potentiometer is \(0.2 \mathrm{~A}\). T he specific resistance and cross-section of the potentiometer wire are \(4 \times 10^{-7} \mathrm{~m}^{2}\), respectively. The potential gradient will be equal to [M ains-2011]

268510 A potentiometer wire\(10 \mathrm{~m}\) long has a resistance of \(40 \Omega\). It is connected in series with a resistanced box and a \(2 \mathrm{v}\) storage cell. If the potential gradient along the wire is \(0.01 \mathrm{~V} / \mathrm{m}\) the resistance unplugged in the box is