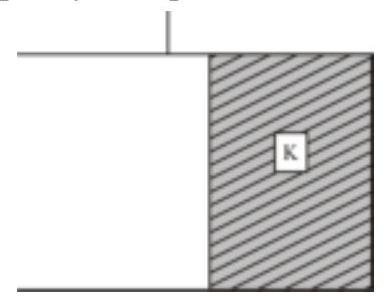
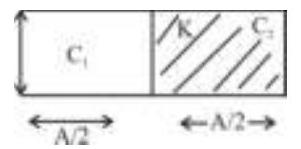
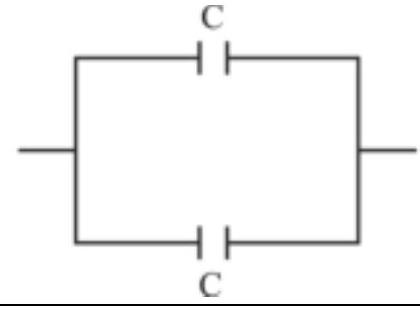
166046 A parallel plate capacitor has a capacity $80 \times$ $10^{-6} \mathrm{~F}$, when air is present between the plates. The volume between the plates is then completely filled with a dielectric slab of dielectric constant 20. The capacitor is now connected to a battery of $30 \mathrm{~V}$ by wires. The dielectric slab is then removed. Then, the charge that passes now through the wire is
166046 A parallel plate capacitor has a capacity $80 \times$ $10^{-6} \mathrm{~F}$, when air is present between the plates. The volume between the plates is then completely filled with a dielectric slab of dielectric constant 20. The capacitor is now connected to a battery of $30 \mathrm{~V}$ by wires. The dielectric slab is then removed. Then, the charge that passes now through the wire is
166046 A parallel plate capacitor has a capacity $80 \times$ $10^{-6} \mathrm{~F}$, when air is present between the plates. The volume between the plates is then completely filled with a dielectric slab of dielectric constant 20. The capacitor is now connected to a battery of $30 \mathrm{~V}$ by wires. The dielectric slab is then removed. Then, the charge that passes now through the wire is
166046 A parallel plate capacitor has a capacity $80 \times$ $10^{-6} \mathrm{~F}$, when air is present between the plates. The volume between the plates is then completely filled with a dielectric slab of dielectric constant 20. The capacitor is now connected to a battery of $30 \mathrm{~V}$ by wires. The dielectric slab is then removed. Then, the charge that passes now through the wire is