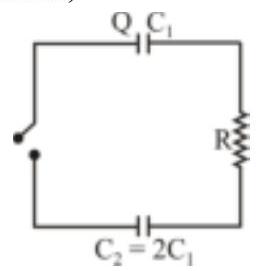
166033
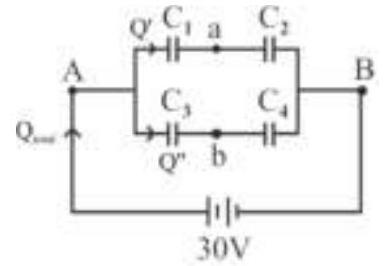
Four capacitors with capacitance $C_{1}=1 \mu \mathrm{F}$, $\mathrm{C}_{2}=1.5 \mu \mathrm{F}, \quad \mathrm{C}_{3}=2.5 \mu \mathrm{F}$ and $\mathrm{C}_{4}=0.5 \mu \mathrm{F}$ are connected as shown in figure to a $30 \mathrm{~V}$ sources. The potential difference between points a and $b$ is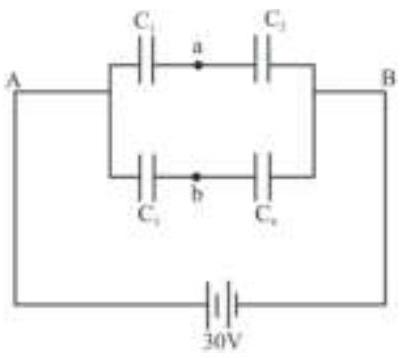
166033
Four capacitors with capacitance $C_{1}=1 \mu \mathrm{F}$, $\mathrm{C}_{2}=1.5 \mu \mathrm{F}, \quad \mathrm{C}_{3}=2.5 \mu \mathrm{F}$ and $\mathrm{C}_{4}=0.5 \mu \mathrm{F}$ are connected as shown in figure to a $30 \mathrm{~V}$ sources. The potential difference between points a and $b$ is
166033
Four capacitors with capacitance $C_{1}=1 \mu \mathrm{F}$, $\mathrm{C}_{2}=1.5 \mu \mathrm{F}, \quad \mathrm{C}_{3}=2.5 \mu \mathrm{F}$ and $\mathrm{C}_{4}=0.5 \mu \mathrm{F}$ are connected as shown in figure to a $30 \mathrm{~V}$ sources. The potential difference between points a and $b$ is
166033
Four capacitors with capacitance $C_{1}=1 \mu \mathrm{F}$, $\mathrm{C}_{2}=1.5 \mu \mathrm{F}, \quad \mathrm{C}_{3}=2.5 \mu \mathrm{F}$ and $\mathrm{C}_{4}=0.5 \mu \mathrm{F}$ are connected as shown in figure to a $30 \mathrm{~V}$ sources. The potential difference between points a and $b$ is