165793
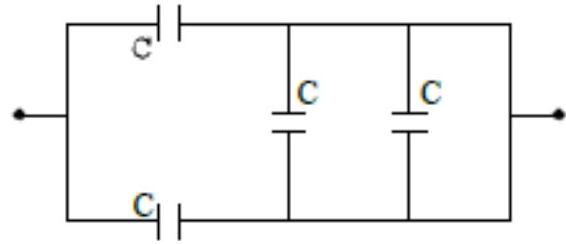
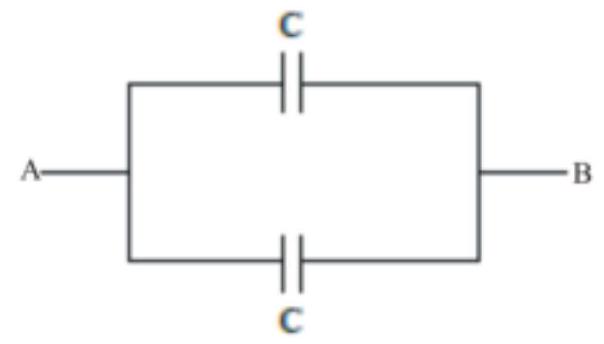
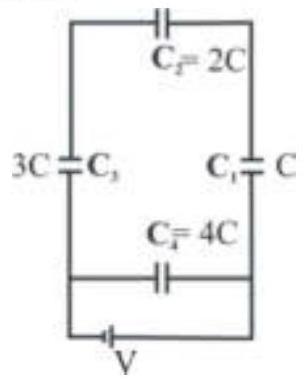
A network of four capacitors of capacity equal to $\mathrm{C}_{1}=\mathrm{C}, \mathrm{C}_{2}=2 \mathrm{C}, \mathrm{C}_{3}=3 \mathrm{C}$ and $\mathrm{C}_{4}=4 \mathrm{C}$ are conducted to a battery as shown in the figure . The ratio of the charges on $\mathrm{C}_{2}$ and $\mathrm{C}_{4}$ is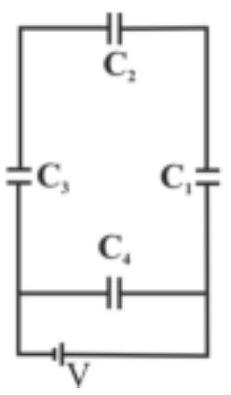
165793
A network of four capacitors of capacity equal to $\mathrm{C}_{1}=\mathrm{C}, \mathrm{C}_{2}=2 \mathrm{C}, \mathrm{C}_{3}=3 \mathrm{C}$ and $\mathrm{C}_{4}=4 \mathrm{C}$ are conducted to a battery as shown in the figure . The ratio of the charges on $\mathrm{C}_{2}$ and $\mathrm{C}_{4}$ is
165793
A network of four capacitors of capacity equal to $\mathrm{C}_{1}=\mathrm{C}, \mathrm{C}_{2}=2 \mathrm{C}, \mathrm{C}_{3}=3 \mathrm{C}$ and $\mathrm{C}_{4}=4 \mathrm{C}$ are conducted to a battery as shown in the figure . The ratio of the charges on $\mathrm{C}_{2}$ and $\mathrm{C}_{4}$ is
165793
A network of four capacitors of capacity equal to $\mathrm{C}_{1}=\mathrm{C}, \mathrm{C}_{2}=2 \mathrm{C}, \mathrm{C}_{3}=3 \mathrm{C}$ and $\mathrm{C}_{4}=4 \mathrm{C}$ are conducted to a battery as shown in the figure . The ratio of the charges on $\mathrm{C}_{2}$ and $\mathrm{C}_{4}$ is
165793
A network of four capacitors of capacity equal to $\mathrm{C}_{1}=\mathrm{C}, \mathrm{C}_{2}=2 \mathrm{C}, \mathrm{C}_{3}=3 \mathrm{C}$ and $\mathrm{C}_{4}=4 \mathrm{C}$ are conducted to a battery as shown in the figure . The ratio of the charges on $\mathrm{C}_{2}$ and $\mathrm{C}_{4}$ is